7. Discrete Transmission Channels

7.1. Exercise 1

Consider a communication process defined by the following joint probability matrix:

\[\begin{split}P(x_i \cap y_j) = \begin{bmatrix} \frac{1}{2} & 0 & 0 \\ 0 & \frac{1}{4} & \frac{1}{4} \\ \end{bmatrix}\end{split}\]

• a). compute the marginal probabilities and the marginal entropies \(H(X)\) and \(H(Y)\);

• b). Find the channel matrix \(P(Y|X)\) and draw the graph of the channel;

• c). compute the mutual information \(I(X,Y)\), and draw the geometrical representation.

7.1.1. Solution

a). compute the marginal probabilities and the marginal entropies \(H(X)\) and \(H(Y)\)

The marginal probabilities are computed by summing the joint probabilities over the rows and columns. The rows correspond to the inputs \(x_i\), and the columns correspond to the outputs \(y_j\).

The marginal probabilities \(p(x_i)\) are found by summing the rows:

\[\begin{split}\begin{align*} p(x_1) &= \frac{1}{2} + 0 + 0 = \frac{1}{2} \\ p(x_2) &= 0 + \frac{1}{4} + \frac{1}{4} = \frac{1}{2} \end{align*}\end{split}\]

The marginal entropy \(H(X)\) is the entropy of the \(p(x_i)\) probabilities:

\[H(X) = -\sum_{i} p(x_i) \log_2 p(x_i) = - \frac{1}{2} \log_2 \frac{1}{2} - \frac{1}{2} \log_2 \frac{1}{2} = 1\]

The marginal probabilities \(p(y_j)\) are found by summing the columns:

\[\begin{split}\begin{align*} p(y_1) &= \frac{1}{2} + 0 = \frac{1}{2} \\ p(y_2) &= 0 + \frac{1}{4} = \frac{1}{4} \\ p(y_3) &= 0 + \frac{1}{4} = \frac{1}{4} \end{align*}\end{split}\]

The marginal entropy \(H(Y)\) is the entropy of the \(p(y_j)\) probabilities:

\[H(Y) = -\sum_{j} p(y_j) = - \frac{1}{2} \log_2 \frac{1}{2} - \frac{1}{4} \log_2 \frac{1}{4} - \frac{1}{4} \log_2 \frac{1}{4} = 1.5\]

b). Find the channel matrix \(P(Y|X)\) and draw the graph of the channel

The channel matrix \(P(Y|X)\) is computed by dividing each row of the joint probability matrix by the corresponding \(p(x_i)\), i.e. by the sum of that row. This is known as “normalization” of the rows. The resulting matrix contains the conditional probabilities \(P(y_j | x_i)\).

Dividing the first row by \(p(x_1) = \frac{1}{2}\) and the second row by \(p(x_2) = \frac{1}{2}\), we get:

\[\begin{split}P(Y|X) = \begin{bmatrix} 1 & 0 & 0 \\ 0 & \frac{1}{2} & \frac{1}{2} \\ \end{bmatrix}\end{split}\]

The graph of the channel is a graphical representation of the channel matrix, where the inputs \(x_i\) are on the left, the outputs \(y_j\) are on the right, and the non-zero probabilities are shown as arrows from inputs to outputs.

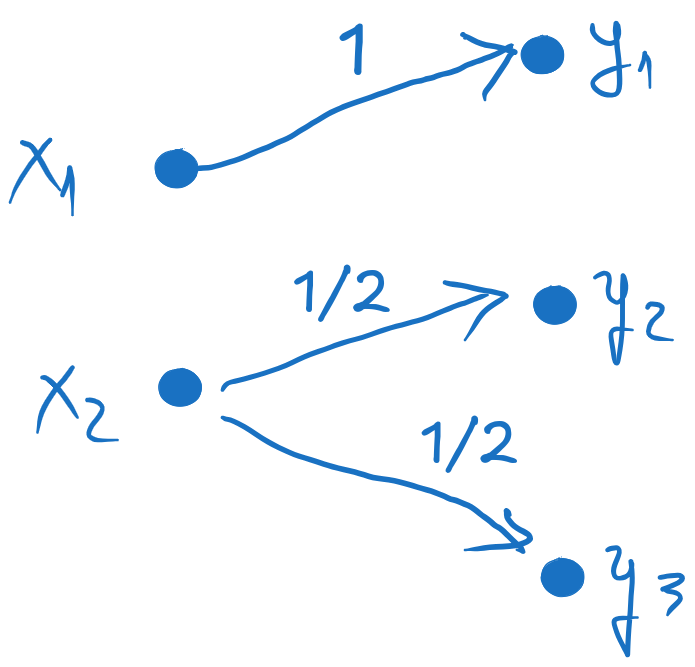
Fig. 7.1 The graph of the channel

c). compute the mutual information \(I(X,Y)\), and draw the geometrical representation

We start from the general relation between the six entropies, discussed in the lecture:

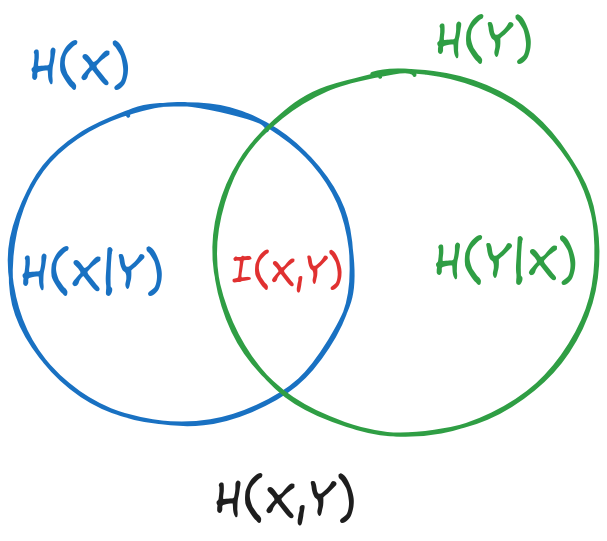
Fig. 7.2 General relation between the six entropies

where:

• \(H(X)\) is the area of the first circle

• \(H(Y)\) is the area of the second circle

• \(H(X,Y)\) is the area of the reunion of the two circles

• \(H(X|Y)\) is the part of the first circle outside of the second circle

• \(H(Y|X)\) is the part of the second circle outside of the first circle

• \(I(X,Y)\) is the intersection of the two circles

Knowing three of the six entropies, we can compute the other three using relations deduced from the figure.

In this case, we already know \(H(X) = 1\) and \(H(Y) = 1.5\) from a). Another easy one is \(H(X,Y)\), which is the entropy of all the values in the joint probability matrix:

\[\begin{split} \begin{align*} H(X,Y) &= -\sum_{i,j} P(x_i \cap y_j) \log_2 P(x_i \cap y_j) \\ &= -\frac{1}{2} \log_2 \frac{1}{2} -\frac{1}{4} \log_2 \frac{1}{4} - \frac{1}{4} \log_2 \frac{1}{4}\\ &= 1.5 \end{align*} \end{split}\]

From the figure, we can see the following relation:

\[I(X,Y) = H(X) + H(Y) - H(X,Y)\]

which gives:

\[I(X,Y) = 1 + 1.5 - 1.5 = 1\]

For the geometrical representation, we observe that \(H(X,Y)\) is equal to \(H(Y)\), which means that the first circle is completely contained in the second circle.

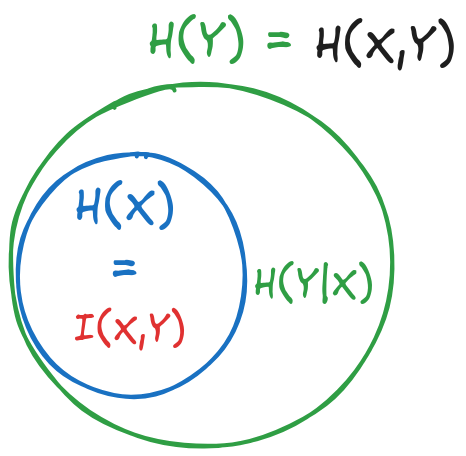
Fig. 7.3 Geometrical representation of the entropies for Exercise 1

7.2. Exercise 2

At the input of a binary symmetric channel with the following channel matrix

\[\begin{split}P(y_j | x_i) = \begin{bmatrix} \frac{2}{3} & \frac{1}{3} \\ \frac{1}{3} & \frac{2}{3} \\ \end{bmatrix}\end{split}\]

we apply two inputs \(x_1\) and \(x_2\) with probabilities \(p(x_1) = \frac{3}{4}\) and \(p(x_2) = \frac{1}{4}\).

• a). Draw the graph of the channel

• b). Find \(H(X)\), \(H(Y)\) and \(I(X,Y)\)

• c). Compute the uncertainty remaining over the input \(X\) when output symbol \(y_2\) is received

• d). Compute the channel capacity, the redundancy and the efficiency of the channel.

7.2.1. Solution

a). Draw the graph of the channel

The graph of the channel is simply a representation of the channel matrix. Here, there are two inputs and two outputs.

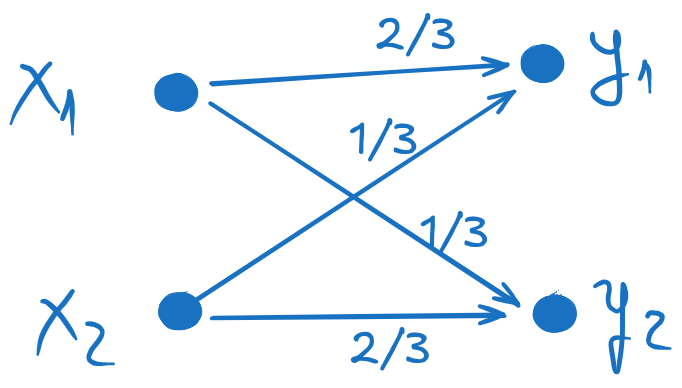
Fig. 7.4 The graph of the channel

b). Find \(H(X)\), \(H(Y)\) and \(I(X,Y)\)

We first need to compute the joint probability matrix \(P(x_i \cap y_j)\). We do this by multiplying the rows of the channel matrix \(P(Y|X)\) by the probabilities of the inputs \(p(x_i)\), each row by the corresponding \(p(x_i)\). This is the opposite of the normalization we did in Exercise 1.

We multiply the first row by \(p(x_1) = \frac{3}{4}\) and the second row by \(p(x_2) = \frac{1}{4}\):

\[\begin{split}P(x_i \cap y_j) = \begin{bmatrix} \frac{1}{2} & \frac{1}{4} \\ \frac{1}{12} & \frac{2}{12} \\ \end{bmatrix}\end{split}\]

Now we do the same as in Exercise 1. We already know the probabilities \(p(x_i)\), so their entropy is:

\[H(X) = -\sum_{i} p(x_i) \log_2 p(x_i) = - \frac{3}{4} \log_2 \frac{3}{4} - \frac{1}{4} \log_2 \frac{1}{4} = 0.811\]

From the joint probability matrix, we can compute the marginal probabilities \(p(y_j)\) and then their entropy:

\[\begin{split}\begin{align*} p(y_1) &= \frac{1}{2} + \frac{1}{12} = \frac{7}{12} \\ p(y_2) &= \frac{1}{4} + \frac{2}{12} = \frac{5}{12} \end{align*}\end{split}\]

\[H(Y) = -\sum_{j} p(y_j) \log_2 p(y_j) = - \frac{7}{12} \log_2 \frac{7}{12} - \frac{5}{12} \log_2 \frac{5}{12} \approx 0.980\]

The joint entropy \(H(X,Y)\) is computed from all the four values in the joint probability matrix:

\[\begin{split} \begin{align*} H(X,Y) &= -\sum_{i,j} P(x_i \cap y_j) \log_2 P(x_i \cap y_j) \\ &= -\frac{1}{2} \log_2 \frac{1}{2} - \frac{1}{4} \log_2 \frac{1}{4} - \frac{1}{12} \log_2 \frac{1}{12} - \frac{2}{12} \log_2 \frac{2}{12} \\ &\approx 1.729 \end{align*} \end{split}\]

The mutual information \(I(X,Y)\) is:

\[I(X,Y) = H(X) + H(Y) - H(X,Y) = 0.811 + 0.980 - 1.729 \approx 0.062\]

c). Compute the uncertainty remaining over the input \(X\) when output symbol \(y_2\) is received

“The uncertainty remaining over the input \(X\) when output symbol \(y_2\) is received” is the conditional entropy \(H(X|y_2)\). This is the entropy of the second column (\(y_2\)) from the matrix \(P(X|Y)\).

To compute the matrix \(P(X|Y)\), we need to normalize the columns joint probability matrix \(P(x_i \cap y_j)\) (i.e. divide each column by its sum, the corresponding marginal probability \(p(y_j)\)).

Normalizing the columns of the joint probability matrix, we get:

\[\begin{split}P(X|Y) = \begin{bmatrix} \frac{6}{7} & \frac{3}{5} \\ \frac{1}{7} & \frac{2}{5} \\ \end{bmatrix}\end{split}\]

The conditional entropy \(H(X|y_2)\) is then the entropy of the second column (note that each column sums to 1, so it is a probability distribution):

\[\begin{split} \begin{align*} H(X|y_2) &= -\sum_{i} P(x_i | y_2) \log_2 P(x_i | y_2) \\ &= - \frac{3}{5} \log_2 \frac{3}{5} - \frac{2}{5} \log_2 \frac{2}{5} \\ &\approx 0.97 \end{align*} \end{split}\]

d). Compute the channel capacity, the redundancy and the efficiency of the channel

This is slightly more difficult and needs some theory from the lectures.

The channel capacity \(C\) is the maximum mutual information \(I(X,Y)\) over all possible input probabilities \(p(x_i)\):

\[ C = \max_{p(x_i)} I(X,Y) \]

We can write \(I(X,Y)\) as \(I(X,Y) = H(Y) - H(Y|X)\), so that:

\[ C = \max_{p(x_i)} (H(Y) - H(Y|X)) \]

We use the fact that the channel is symmetric, i.e. it is uniform with respect to the input and also uniform with respect to the output (see the lecture for more on this).

Since the channel is uniform with respect to the input, \(H(Y|X)\) does not depend on the input probabilities \(p(x_i)\), and is constant (see lectures). As such, it goes out of the maximization above, and we can write:

\[ C = \max_{p(x_i)} H(Y) - H(Y|X) \]

where the the maximum is only for the term \(H(Y)\).

The entropy \(H(Y)\) is maximum when the probabilities \(p(y_j)\) are equal. Since the channel is also uniform with respect to the output, the consequence is that “If the input symbols are equiprobable, the output symbols are also equiprobable” (see the lecture). Therefore, the maximum value of \(H(Y)\) is achieved when \(p(x_1) = p(x_2) = \frac{1}{2}\), which implies that \(p(y_1) = p(y_2) = \frac{1}{2}\). Therefore, the maximum value of \(H(Y)\) is:

\[ \max H(Y) = -\frac{1}{2} \log_2 \frac{1}{2} - \frac{1}{2} \log_2 \frac{1}{2} = 1 \]

The constant \(H(Y|X)\) can be computed with one of the usual relations:

\[ H(Y|X) = H(Y) - I(X,Y) = 0.980 - 0.062 = 0.918 \]

The channel capacity is then:

\[ C = \max_{p(x_i)} H(Y) - H(Y|X) = 1 - 0.918 = 0.082 \;\; bits \]

The efficiency of the channel is the ratio between the current \(I(X,Y)\) and the channel capacity \(C\):

\[\begin{split} \begin{align*} \eta &= \frac{I(X,Y)}{C} = \frac{0.062}{0.082} \approx 0.756 \\ \rho &= 1 - \eta = 0.244 \end{align*} \end{split}\]

7.3. Exercise 3

Consider a communication process with 2 inputs and 3 outputs. The inputs and output events have equal probabilities, and are independent.

• a). Write the joint probability matrix

• b). Draw the graph of the channel (together with the probabilities)

• c). Compute the marginal entropies and the joint entropy, and verify that

  \[H(X,Y) = H(X) + H(Y)\]

  and that

  \[I(X,Y) = 0\]

7.3.1. Solution

a). Write the joint probability matrix

The input and output events are independent means that the joint probability is just the product of the two separate probabilities:

\[P(x_i \cap y_j) = P(x_i) \cdot P(y_j)\]

Since the inputs and outputs have equal probabilities, it means that \(p(x_1) = p(x_2) = \frac{1}{2}\) and \(p(y_1) = p(y_2) = p(y_3) = \frac{1}{3}\). The joint probability matrix is then:

\[\begin{split}P(x_i \cap y_j) = \begin{bmatrix} \frac{1}{6} & \frac{1}{6} & \frac{1}{6} \\ \frac{1}{6} & \frac{1}{6} & \frac{1}{6} \\ \end{bmatrix}\end{split}\]

b). Draw the graph of the channel (together with the probabilities)

We obtain the channel matrix \(P(Y|X)\) by dividing each row of the joint probability matrix to its corresponding marginal probability \(p(x_i)\). This results in:

\[\begin{split}P(Y|X) = \begin{bmatrix} \frac{1}{3} & \frac{1}{3} & \frac{1}{3} \\ \frac{1}{3} & \frac{1}{3} & \frac{1}{3} \\ \end{bmatrix} \end{split}\]

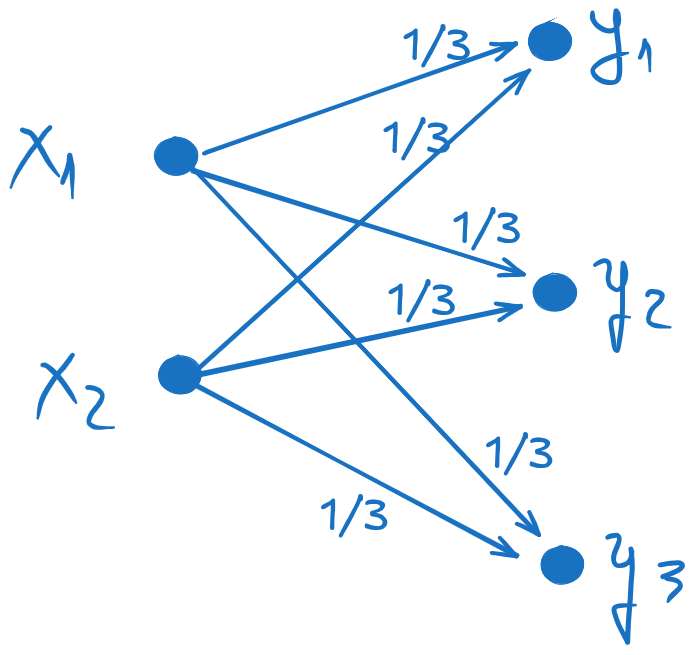
Fig. 7.5 The graph of the channel

c). Compute the marginal entropies and the joint entropy, and verify that \(H(X,Y) = H(X) + H(Y)\) and that \(I(X,Y) = 0\)

We know the probabilities \(p(x_i)\) and \(p(y_j)\), so we can compute the marginal entropies. The joint entropy \(H(X,Y)\) is computed from all the six values in the joint probability matrix.

\[\begin{split}\begin{align*} H(X) &= -\sum_{i} p(x_i) \log_2 p(x_i) = - 2 \cdot \frac{1}{2} \log_2 \frac{1}{2} = 1 \\ H(Y) &= -\sum_{j} p(y_j) \log_2 p(y_j) = - 3 \cdot \frac{1}{3} \log_2 \frac{1}{3} = 1.585 \\ H(X,Y) &= -\sum_{i,j} P(x_i \cap y_j) \log_2 P(x_i \cap y_j) \\ &= -6 \cdot \frac{1}{6} \log_2 \frac{1}{6} = 2.585 \end{align*}\end{split}\]

We can verify that \(H(X,Y) = H(X) + H(Y)\) since

\[H(X,Y) = \log_2 6 = \log_2 (2 \cdot 3) = \log_2 2 + \log_2 3 = H(X) + H(Y)\]

The mutual information \(I(X,Y)\) is then 0:

\[I(X,Y) = H(X) + H(Y) - H(X,Y) = 0\]

This is to be expected, since the inputs and outputs are independent, and this means that there is no relation between the inputs and outputs of the channel. Therefore the communication is useless, and no information is transmitted at all.

7.4. Exercise 4

Give an example of a channel having 3 inputs and 3 outputs, with \(H(Y|X) = 0\) (write the channel matrix).

7.4.1. Solution

3 inputs and 3 outputs means a channel matrix \(P(Y|X)\) with 3 rows and 3 columns.

\(H(Y|X) = 0\) means zero uncertainty about the output when the input is known. This means that there is a single arrow from each input \(x_i\) to a single output \(y_j\). The probability must then be 1.

Below is a possible example of such a channel:

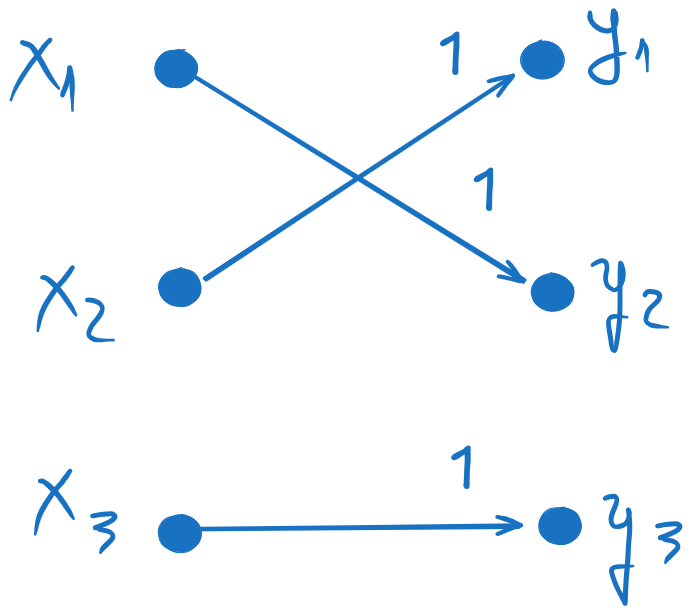
Fig. 7.6 The graph of the channel

\[\begin{split}P(Y|X) = \begin{bmatrix} 0 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \\ \end{bmatrix}\end{split}\]

7.5. Exercise 5

Give an example of a channel with two inputs, such that \(H(Y|x_1) \neq 0\) and \(H(Y|x_2) = 0\) (write the channel matrix).

7.5.1. Solution

\(H(Y|x_1)\) is the entropy computed from the first row of the channel matrix \(P(Y|X)\). It must be non-zero, which means that there should be at least two non-zero probabilities.

\(H(Y|x_2)0\) is the entropy computed from the second row of the channel matrix \(P(Y|X)\), and since it is zero, there must be a single value of 1 and all the others must be 0.

Therefore, a possible channel matrix, with two inputs and two outputs, is:

\[\begin{split}P(Y|X) = \begin{bmatrix} \frac{1}{2} & \frac{1}{2} \\ 1 & 0 \\ \end{bmatrix}\end{split}\]