8. Computing entropy of files#
8.1. Introduction#
In this application we treat a file like a sequence of bytes generated by a Discrete Memoryless Source (DMS).
We estimate the entropy of the file by computing the empirical frequency of each byte, and then using the formula for the entropy of a DMS.
where \(p_i\) is the frequency of the byte \(i\) in the file.
8.2. Walkthrough#
We estimate the frequency of every byte by counting.
First, let’s open a file and read its content, incrementing
a counter for each byte.
We’re going to use the read_bytes() metod available in Pathlib package.
import pathlib
filename = "data/texten.txt"
# Prepare counters
counts = [0] * 256
for byte in pathlib.Path(filename).read_bytes():
counts[byte] += 1
Now, let’s print some statistics about the counters:
print(f"Total bytes = {sum(counts)}")
print(f"{'Code':>10} {'Char':>10} {'Count':>10}")
for i, count in enumerate(counts):
if chr(i).isalpha():
print(f"{i:>10d} {i:>10c} {count:>10d}")
Total bytes = 16407
Code Char Count
65 A 147
66 B 88
67 C 57
68 D 63
69 E 110
70 F 29
71 G 58
72 H 45
73 I 228
74 J 3
75 K 5
76 L 54
77 M 44
78 N 59
79 O 190
80 P 19
81 Q 0
82 R 111
83 S 70
84 T 128
85 U 12
86 V 13
87 W 48
88 X 1
89 Y 22
90 Z 2
97 a 697
98 b 127
99 c 202
100 d 360
101 e 1164
102 f 211
103 g 181
104 h 632
105 i 615
106 j 7
107 k 75
108 l 355
109 m 262
110 n 624
111 o 863
112 p 134
113 q 7
114 r 613
115 s 653
116 t 827
117 u 363
118 v 117
119 w 189
120 x 8
121 y 237
122 z 3
170 ª 0
181 µ 0
186 º 0
192 À 0
193 Á 0
194 Â 0
195 Ã 0
196 Ä 0
197 Å 0
198 Æ 0
199 Ç 0
200 È 0
201 É 0
202 Ê 0
203 Ë 0
204 Ì 0
205 Í 0
206 Î 0
207 Ï 0
208 Ð 0
209 Ñ 0
210 Ò 0
211 Ó 0
212 Ô 0
213 Õ 0
214 Ö 0
216 Ø 0
217 Ù 0
218 Ú 0
219 Û 0
220 Ü 0
221 Ý 0
222 Þ 0
223 ß 0
224 à 0
225 á 0
226 â 0
227 ã 0
228 ä 0
229 å 0
230 æ 0
231 ç 0
232 è 0
233 é 0
234 ê 0
235 ë 0
236 ì 0
237 í 0
238 î 0
239 ï 0
240 ð 0
241 ñ 0
242 ò 0
243 ó 0
244 ô 0
245 õ 0
246 ö 0
248 ø 0
249 ù 0
250 ú 0
251 û 0
252 ü 0
253 ý 0
254 þ 0
255 ÿ 0
Let’s print a histogram of the letter counters.
import matplotlib.pyplot as plt
chars_hist = [chr(i) for i in range(65, 122)]
count_hist = [counts[i] for i in range(65, 122)]
plt.bar(chars_hist, count_hist)
plt.show()
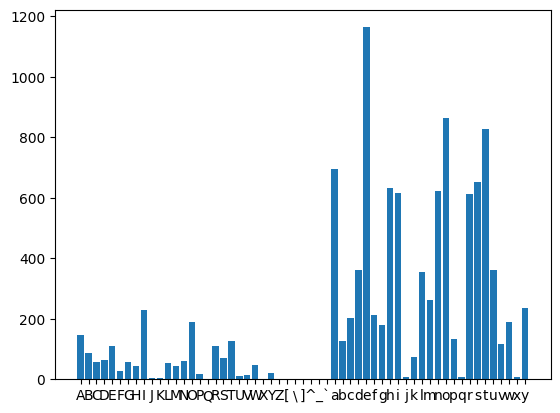
We obtain probabilities by dividing each counter to the total:
probs = [count / sum(counts) for count in counts]
print(f"{'Code':>10} {'Char':>10} {'Count':>10} {'Prob':>10}")
for i, (count, prob) in enumerate(zip(counts, probs)):
if chr(i).isalpha():
print(f"{i:>10d}{i:>10c}{count:>10d}{prob:>20.6f}")
Code Char Count Prob
65 A 147 0.008960
66 B 88 0.005364
67 C 57 0.003474
68 D 63 0.003840
69 E 110 0.006704
70 F 29 0.001768
71 G 58 0.003535
72 H 45 0.002743
73 I 228 0.013897
74 J 3 0.000183
75 K 5 0.000305
76 L 54 0.003291
77 M 44 0.002682
78 N 59 0.003596
79 O 190 0.011580
80 P 19 0.001158
81 Q 0 0.000000
82 R 111 0.006765
83 S 70 0.004266
84 T 128 0.007802
85 U 12 0.000731
86 V 13 0.000792
87 W 48 0.002926
88 X 1 0.000061
89 Y 22 0.001341
90 Z 2 0.000122
97 a 697 0.042482
98 b 127 0.007741
99 c 202 0.012312
100 d 360 0.021942
101 e 1164 0.070945
102 f 211 0.012860
103 g 181 0.011032
104 h 632 0.038520
105 i 615 0.037484
106 j 7 0.000427
107 k 75 0.004571
108 l 355 0.021637
109 m 262 0.015969
110 n 624 0.038033
111 o 863 0.052600
112 p 134 0.008167
113 q 7 0.000427
114 r 613 0.037362
115 s 653 0.039800
116 t 827 0.050405
117 u 363 0.022125
118 v 117 0.007131
119 w 189 0.011519
120 x 8 0.000488
121 y 237 0.014445
122 z 3 0.000183
170 ª 0 0.000000
181 µ 0 0.000000
186 º 0 0.000000
192 À 0 0.000000
193 Á 0 0.000000
194 Â 0 0.000000
195 Ã 0 0.000000
196 Ä 0 0.000000
197 Å 0 0.000000
198 Æ 0 0.000000
199 Ç 0 0.000000
200 È 0 0.000000
201 É 0 0.000000
202 Ê 0 0.000000
203 Ë 0 0.000000
204 Ì 0 0.000000
205 Í 0 0.000000
206 Î 0 0.000000
207 Ï 0 0.000000
208 Ð 0 0.000000
209 Ñ 0 0.000000
210 Ò 0 0.000000
211 Ó 0 0.000000
212 Ô 0 0.000000
213 Õ 0 0.000000
214 Ö 0 0.000000
216 Ø 0 0.000000
217 Ù 0 0.000000
218 Ú 0 0.000000
219 Û 0 0.000000
220 Ü 0 0.000000
221 Ý 0 0.000000
222 Þ 0 0.000000
223 ß 0 0.000000
224 à 0 0.000000
225 á 0 0.000000
226 â 0 0.000000
227 ã 0 0.000000
228 ä 0 0.000000
229 å 0 0.000000
230 æ 0 0.000000
231 ç 0 0.000000
232 è 0 0.000000
233 é 0 0.000000
234 ê 0 0.000000
235 ë 0 0.000000
236 ì 0 0.000000
237 í 0 0.000000
238 î 0 0.000000
239 ï 0 0.000000
240 ð 0 0.000000
241 ñ 0 0.000000
242 ò 0 0.000000
243 ó 0 0.000000
244 ô 0 0.000000
245 õ 0 0.000000
246 ö 0 0.000000
248 ø 0 0.000000
249 ù 0 0.000000
250 ú 0 0.000000
251 û 0 0.000000
252 ü 0 0.000000
253 ý 0 0.000000
254 þ 0 0.000000
255 ÿ 0 0.000000
Finally, let’s compute the entropy. We skip all frequencies equal to zero, since they don’t contribute to the entropy.
from math import log2
entropy = sum([-p * log2(p) for p in probs if p > 0])
print(f"Entropy = {entropy:.2f} bits per byte")
Entropy = 4.53 bits per byte
8.3. Function#
We will encapsulate the code in a function, so that we can reuse it conveniently
def entropy_of_file(filename):
counts = [0] * 256
for byte in pathlib.Path(filename).read_bytes():
counts[byte] += 1
probs = [count / sum(counts) for count in counts]
return sum([-p * log2(p) for p in probs if p > 0])
Now let’s compute the entropy of various files:
entropy_of_file("data/texten.txt")
4.534092589335551
entropy_of_file("data/textro.txt")
4.569350422640342
entropy_of_file("data/Ceahlau.jpg")
7.96649855933222
entropy_of_file("data/ChromeSetup.exe")
7.898282999757679

