8 Seminar 01: Variabile aleatoare și probabilități
8.1 Exercițiul 1
Fie A o variabilă aleatoare continuă cu distribuția \(\mathcal{U}[0, \; 6]\) (distribuție uniformă între 0 și 6).
- a). Reprezentați grafic funcția densitate de probabilitate a lui A (distribuția lui A)
- b). Calculați probabilitatea \(P(A > 1)\)
- c). Calculați probabilitatea \(P(A \in (0, \; 2))\)
- d). Reprezentați funcția de repartiție \(F_A(x)\) și scrieți-i expresia matematică
- e). Care e distribuția variabilei aleatoare \(B\) definită ca \(B = A - 2\)?
- f). Care e distribuția variabilei aleatoare \(C\) definită ca \(C = 3*A\)?
Rezolvare
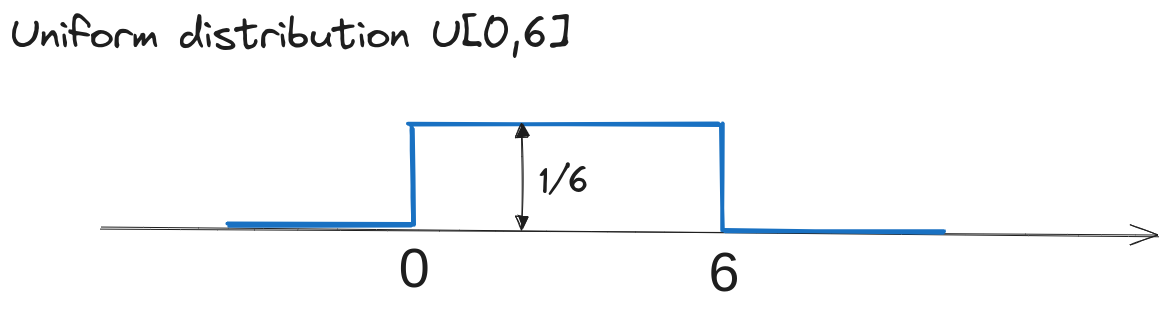
a). Distribuția uniformă \(\mathcal{U}[0, \; 6]\) este reprezentată grafic mai jos.
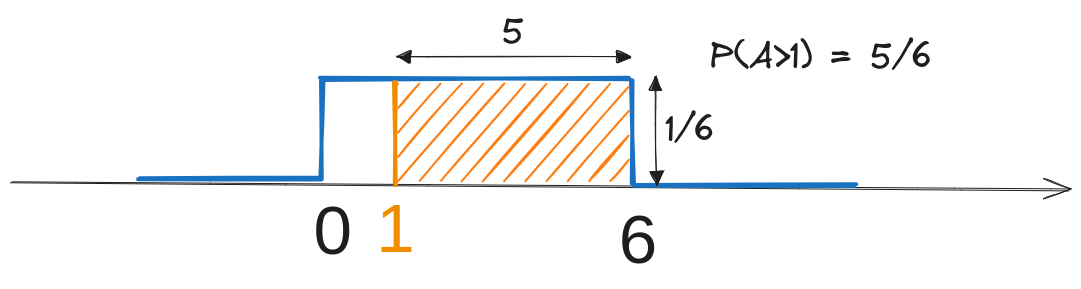
b). Probabilitatea \(P(A > 1)\) reprezintă aria de sub densitatea de probabilitate \(w_A(x)\), de la 1 la infinit (aici, până la 6).
 \[\begin{aligned}
P(A > 1) = \int_{1}^{\infty} w_A(x) dx = \int_{1}^{6} \frac{1}{6} dx = \frac{5}{6}
\end{aligned}\]
\[\begin{aligned}
P(A > 1) = \int_{1}^{\infty} w_A(x) dx = \int_{1}^{6} \frac{1}{6} dx = \frac{5}{6}
\end{aligned}\]
c). Probabilitatea \(P(A \in (0, \; 2))\) reprezintă aria de sub densitatea de probabilitate \(w_A(x)\), de la 0 la 2. 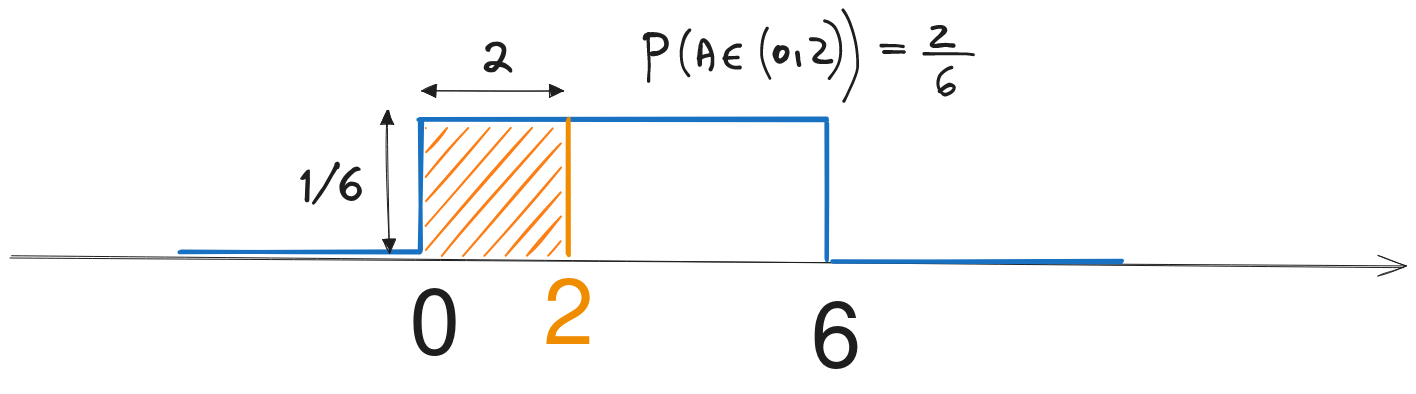 \[\begin{aligned}
P(A \in (0, \; 2)) = \int_{0}^{2} w_A(x) dx = \int_{0}^{2} \frac{1}{6} dx = \frac{1}{3}
\end{aligned}\]
\[\begin{aligned}
P(A \in (0, \; 2)) = \int_{0}^{2} w_A(x) dx = \int_{0}^{2} \frac{1}{6} dx = \frac{1}{3}
\end{aligned}\]
d). Funcția de repartiție \(F_A(x)\) este integrala de la \(-\infty\) la \(x\) a densității de probabilitate \(w_A\). Întrucât \(w_A(x)\) este constantă între 0 și 6, \(F_A(x)\) este o funcție liniară între 0 și 6, și constantă în afara acestui interval.
Așadar, graficul funcției de repartiție, este cel de mai jos.
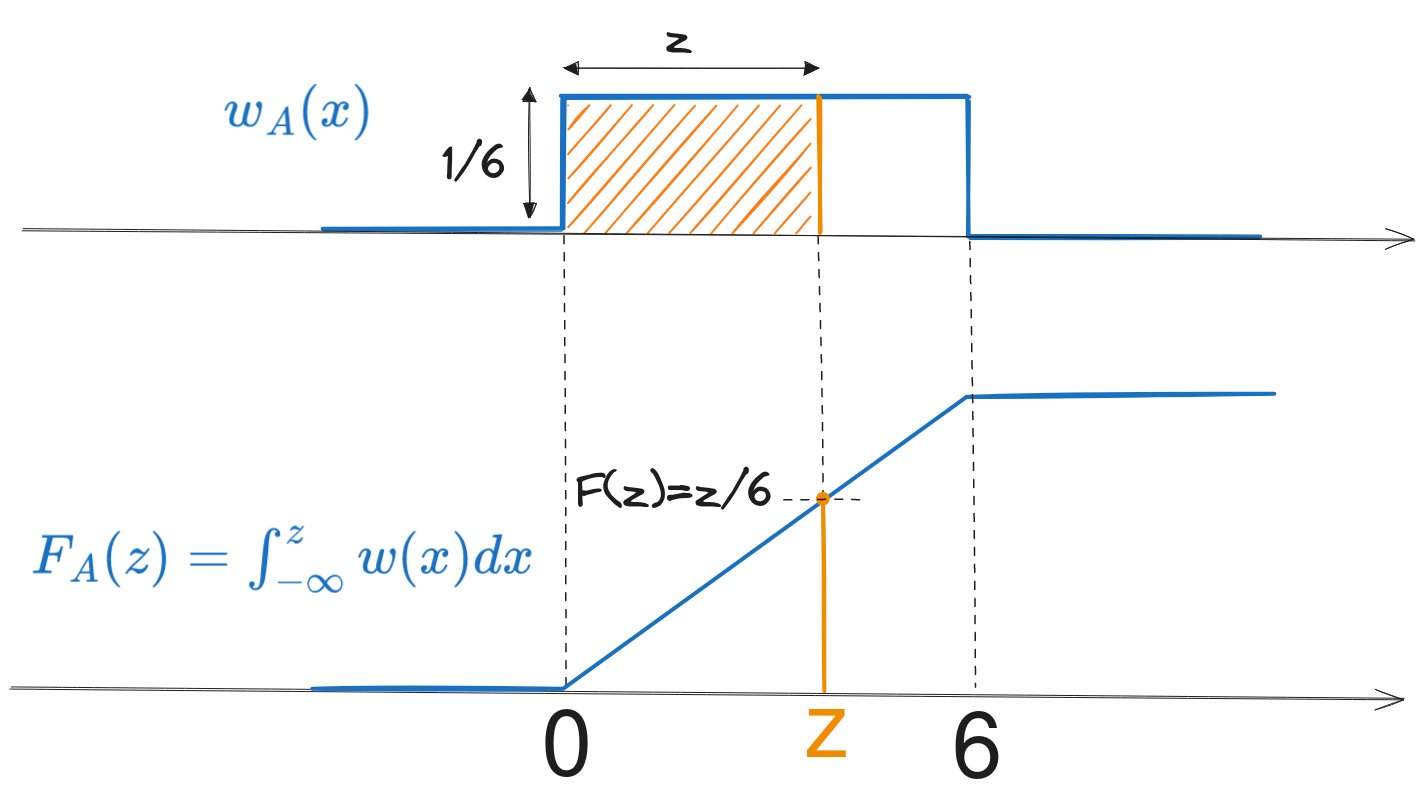
Expresia matematică este: \[F_A(x) = \begin{cases} 0, &x \leq 0 \\ \frac{1}{6}x, &x \in (0, \; 6) \\ 1, &x \geq 6 \end{cases}\]
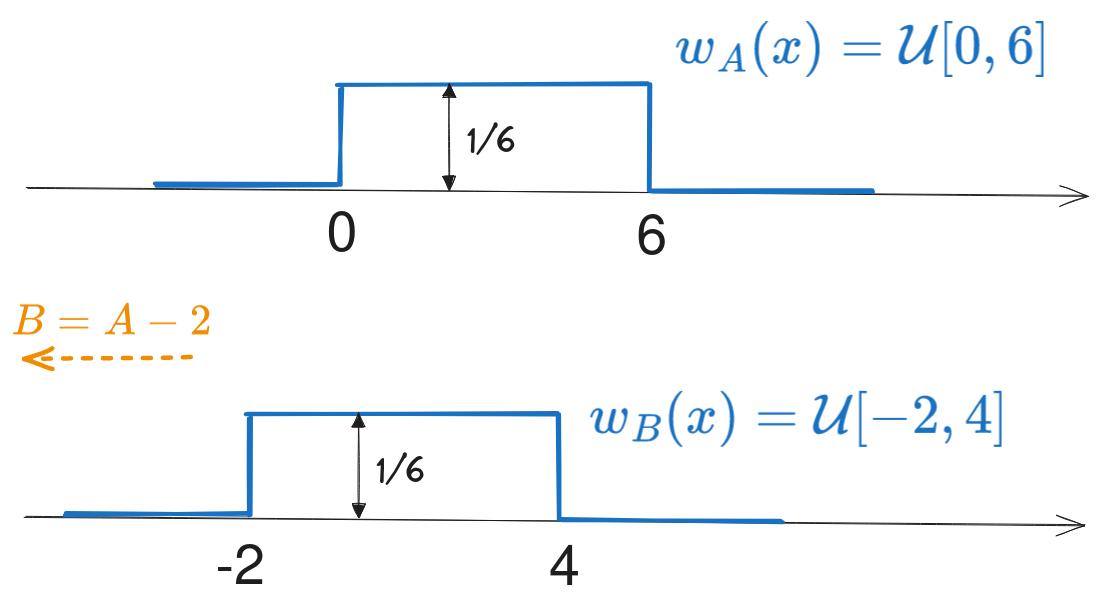
e). Distribuția variabilei aleatoare \(B\) este distribuția variabilei \(A\) translatată cu 2 unități la stânga, așadar o distribuție uniformă între -2 și 4, \(\mathcal{U}[-2, \; 4]\).
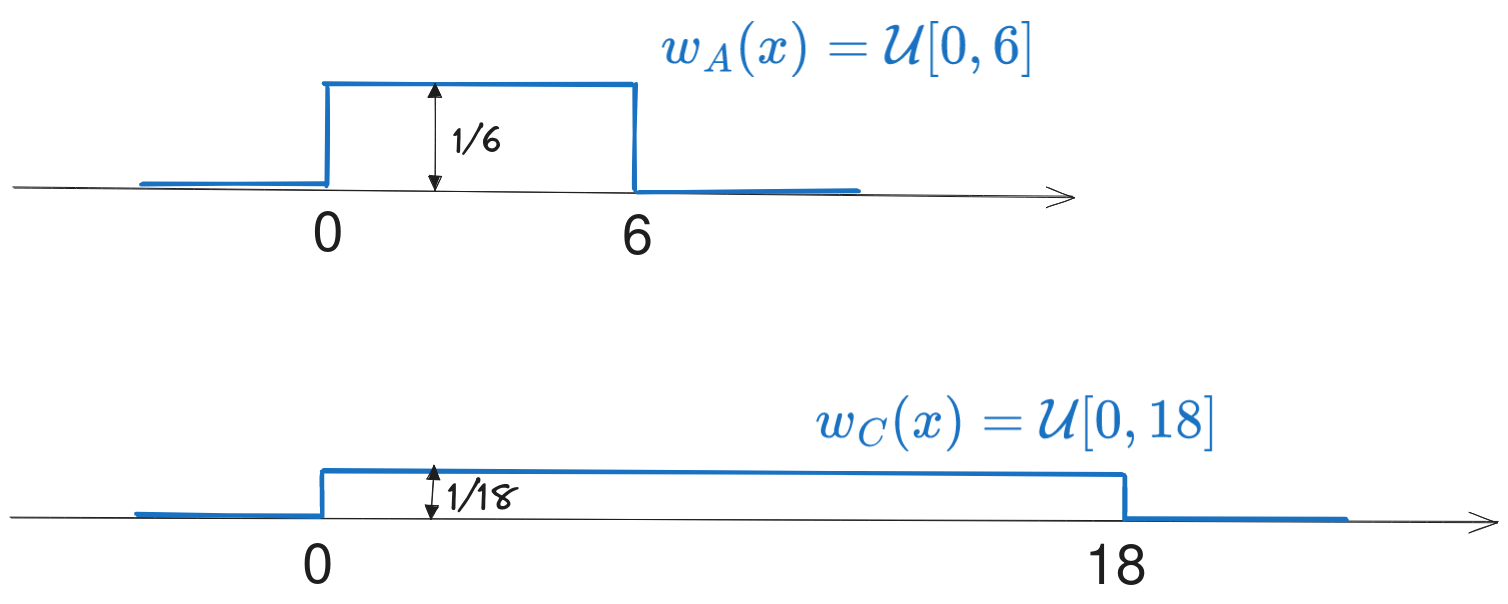
f). Distribuția variabilei aleatoare \(C\) este distribuția variabilei \(A\) scalată cu 3. Dacă \(A\) ia valori între 0 și 6, atunci \(C=3A\) ia valori între 0 și 18, având așadar o distribuție uniformă între 0 și 18, \(\mathcal{U}[0, \; 18]\).
8.2 Exercițiul 2
Fie A o variabilă aleatoare continuă cu distribuția normală \(\mathcal{N}(\mu = 1, \sigma^2 = 20)\).
- a). Calculați probabilitatea \(P(A \in [2, \; 4])\)
- b). Care e distribuția variabilei aleatoare \(B\) definită ca \(B = A - 2\)?
- c). Care este valoarea maximă a distribuției \(w_A(x)\), și pentru ce valoare \(x\) se atinge?
- d). (**) Care e distribuția variabilei aleatoare \(C\) definită ca \(C = 3*A\)?
Rezolvare
a). Probabilitatea \(P(A \in [2, \; 4])\) reprezintă aria de sub densitatea de probabilitate \(w_A(x)\), de la 2 la 4. \[P(A \in [2, \; 4]) = \int_{2}^{4} w_A(x) dx = F(4) - F(2)\] unde \(F(x)\) este funcția de repartiție a lui \(A\), care se poate calcula cu formula: \[F(x) = \frac{1}{2} \left(1 + erf \left(\frac{x - \mu}{\sqrt{2}\sigma}\right)\right)\]
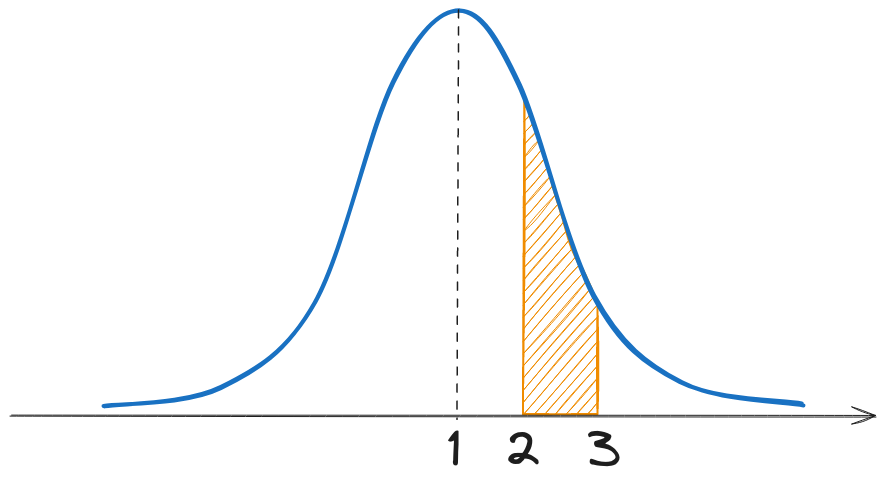
Așadar: \[\begin{aligned} P(A \in [2, \; 4]) &= F(4) - F(2) \\ &= \frac{1}{2} \left(1 + erf \left(\frac{4 - 1}{\sqrt{2}\sqrt{20}}\right)\right) - \frac{1}{2} \left(1 + erf \left(\frac{2 - 1}{\sqrt{2}\sqrt{20}}\right)\right) \\ &= ... \end{aligned}\]
- Distribuția variabilei aleatoare \(B\) este distribuția variabilei \(A\) translatată cu 2 unități la stânga, așadar o distribuție normală cu media -1 și cu aceeași varianță, \(\mathcal{N}(\mu = -1, \sigma^2 = 20)\).
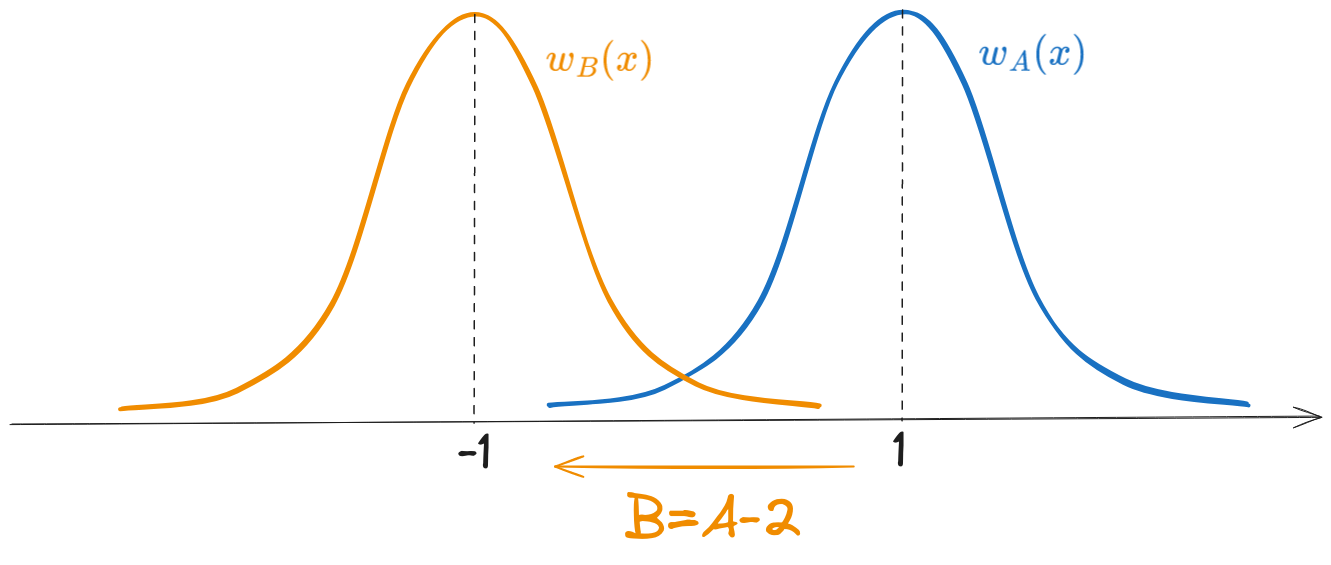
- Inspectând graficul funcției de densitate normală, se observă că maximul este atins întotdeauna în dreptul mediei. Aici, media are valoarea 1, deci maximul este: \[w_A(1) = \frac{1}{\sqrt{40 \pi}} e^{-\frac{(1 - 1)^2}{40}} = \frac{1}{\sqrt{40 \pi}} e^{-0} = \frac{1}{\sqrt{40 \pi}}\]
d). Dacă valorile lui \(C\) sunt triplul valorilor \(A\), atunci am fi tentați să spunem că probabilitatea ca \(C\) să fie în jurul unei valori \(x\) este egală cu probabilitatea ca \(A\) să ia valori în jurul lui \(\frac{x}{3}\). Acest lucru s-ar traduce prin relația: \[w_C(x) = w_A\left(\frac{x}{3}\right)\] Întrucăt \(A\) urmează o distribuție normală, am avea: \[\begin{aligned} w_C(x) &= w_A\left(\frac{x}{3}\right) = \frac{1}{\sqrt{40 \pi}} e^{-\frac{\left(\frac{x}{3} - 1\right)^2}{40}} \\ &= \frac{1}{\sqrt{40 \pi}} e^{-\frac{\left(x - 3\right)^2}{9 \cdot 40}} \\ \end{aligned}\]
Din pacate aici întâlnim o problemă, pentru că expresia la care am ajuns nu este o distribuție Gaussiană, întrucât \(\sigma\) de la exponent (unde \(2 \sigma^2\) este \(9 \cdot 40\)) este diferit de \(\sigma\) din numitorul fracției din față (unde \(\sigma \sqrt{2 \pi} = \sqrt{40 \pi}\)).
În realitate, ne induce în eroare faptul că “a lua valori în jurul lui \(x\)” este o formulare imprecisă, și însăși relația de la care am pornit, \(w_C(x) = w_A\left(\frac{x}{3}\right)\), este incorectă.
Pentru o rezolvare corectă, ne întoarcem la definiția funcției de repartiție, pe care o putem defini întotdeauna în mod riguros: \(F(x) = P\left( X \leq x \right)\).
Așadar, dacă \(C\) este triplul lui \(A\), atunci \(C \leq x\) este totuna cu \(A \leq \frac{x}{3}\), deci probabilitatea \(F_C(x) = P \left(C \leq x \right)\) este în mod riguros aceeași cu \(F_A\left(\frac{x}{3}\right) = P \left(A \leq \frac{x}{3} \right)\): \[F_C(x) = F_A\left(\frac{x}{3}\right)\]
Densitatea de probabilitate este derivata funcției de repartiție, așadar: \[\begin{aligned} w_C(x) &= \frac{d}{dx} F_C(x) = \frac{d}{dx} F_A\left(\frac{x}{3}\right) \\ &= \frac{d}{dx} F_A\left(\frac{x}{3}\right) \cdot \frac{1}{3} \\ &= \frac{1}{3} w_A\left(\frac{x}{3}\right) \\ &= \frac{1}{3} \frac{1}{\sqrt{40 \pi}} e^{-\frac{\left(\frac{x}{3} - 1\right)^2}{40}} \\ &= \frac{1}{3} \frac{1}{\sqrt{40 \pi}} e^{-\frac{\left(x - 3\right)^2}{9 \cdot 40}} \\ &= \frac{1}{3\sqrt{20} \sqrt{2 \pi}} e^{-\frac{\left(x - 3\right)^2}{2 \cdot 9 \cdot 20}} \\ &= \frac{1}{\sigma_C \sqrt{2 \pi}} e^{-\frac{\left(x - \mu_C\right)^2}{2 \cdot \sigma_C^2}} \\ \end{aligned}\]
Recunoaștem în rezultatul de mai sus o distribuție normală, cu media \(\mu_C = 3\) și cu deviația standard \(\sigma_C = 3 \sqrt{20}\), adică \(\sigma_C^2 = 9 \cdot 20\).
Așadar, la triplarea valorilor lui \(A\), obținem o distribuție normală cu \(\mu\) triplat și \(\sigma\) triplat (deci \(\sigma^2\) de 9 ori mai mare): \[w_C(x) = \mathcal{N}(\mu = 3, \sigma^2 = 9 \cdot 20)\]
Rezultatul de mai sus se poate generaliza.
Dacă o variabilă aleatoare cu distribuție normală se scalează cu o orice constantă \(c\), rezultatul va urma tot o distribuție normală, având media scalată cu \(c\) și deviația standard scalată cu \(c\) (varianța \(\sigma^2\) scalată cu \(c^2\)): \[c \cdot \mathcal{N}(\mu, \sigma^2) = \mathcal{N}(c \cdot \mu, c^2 \cdot \sigma^2)\]
În plus, aceeași metodă bazată pe funcția de repartiție se poate folosi și pentru alte distribuții, cum ar fi cea uniformă.
Temă pentru acasă: folosind aceeași metodă, demonstrați riguros că dacă o variabilă aleatoare cu distribuția uniformă \(\mathcal{U}[a, \; b]\) este scalată cu o constantă \(c\), rezultatul urmează o distribuție uniformă \(\mathcal{U}[c \cdot a, \; c \cdot b]\).
8.3 Exercițiul 3
Considerând că scorul IQ urmează o distribuție \(\mathcal{N} \; \left(\mu=100, \sigma=15\right)\), calculați:
- a). Probabilitatea ca o persoană oarecare să aibă IQ > 130
- b). Dacă populația globului este 8 miliarde, câți oameni au IQ mai mic decât 75
- c). (**)Ce IQ minim trebuie să ai pentru a fi între primii 2%?
Rezolvare
a). Probabilitatea ca o persoană oarecare să aibă IQ > 130 este: \[\begin{aligned} P(IQ > 130) &= \int_{130}^{\infty} w_{IQ}(x) dx \\ &= F_{IQ}(\infty) - F_{IQ}(130) \\ &= 1 - \frac{1}{2} \left(1 + erf \left(\frac{130 - 100}{\sqrt{2}\cdot 15}\right)\right) \\ &= 0.0227 = 2.27\% \end{aligned}\]
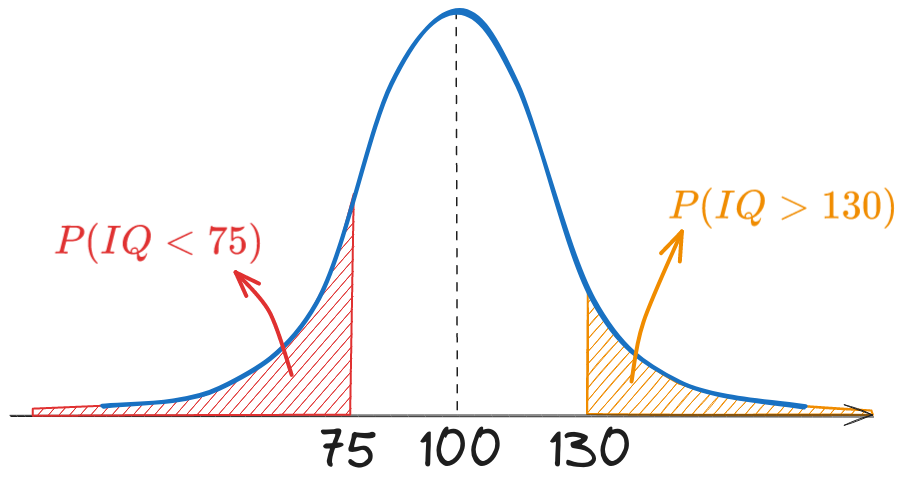
b). Trebuie să calculăm probabilitatea ca o persoană oarecare să aibă IQ < 75, și să înmulțim cu populația globului: \[\begin{aligned} P(IQ < 75) &= \int_{-\infty}^{75} w_{IQ}(x) dx \\ &= F_{IQ}(75) - F_{IQ}(-\infty) \\ &= \frac{1}{2} \left(1 + erf \left(\frac{75 - 100}{\sqrt{2}\cdot 15}\right)\right) \\ &= 0.0478 \end{aligned}\] Așadar, numărul de oameni cu IQ < 75 este: \[8 \cdot 10^9 \cdot 0.0478 = 382.4 \cdot 10^6 = 382.4 \; milioane\]
8.4 Exercițiul 4
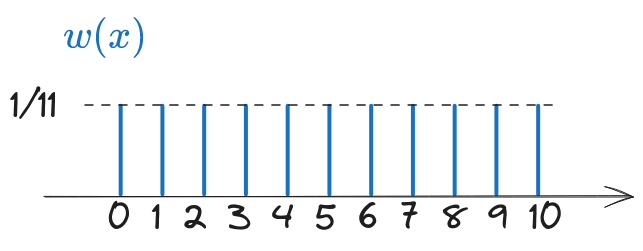
Fie A o variabilă aleatoare discretă, cu valorile posibile \(\left\lbrace 0, 1, 2, \dots 10 \right\rbrace\), toate având aceeași probabilitate.
- a). Reprezentați grafic distribuția lui A
- b). Calculați probabilitatea \(P(A \in [3, \; 7]\)
- b). Care e probabilitatea ca A să fie număr impar?
Rezolvare
- Avem 11 valori posibile, toate cu aceeași probabilitate, așadar distribuția lui A este o distribuție uniformă discretă, \(\mathcal{U}[0, \; 10]\). Fiecare realizare are probabilitatea \(\frac{1}{11}\).
- Fiind o variabilă discretă, putem calcula probabilitățile prin adunarea probabilităților cazurilor favorabile.
Probabilitatea ca \(A\) să ia valori între 3 și 7 este sume celor 5 probabilități din dreptul valorile 3, 4, 5, 6 și 7: \[P(A \in [3, \; 7]) = \frac{5}{11}\]
c). Probabilitatea ca \(A\) să fie impar este suma probabilităților din dreptul valorilor 1, 3, 5, 7, 9: \[P(A \; \text{impar}) = \frac{5}{11}\]
8.5 Exercițiul 5
Calculați probabilitatea ca 3 variabile aleatoare X, Y, Z, independente și identic distribuite (i.i.d) cu distribuția normală \(\mathcal{N}(\mu = 1, \sigma^2 = 1)\) să fie pozitive simultan.
Rezolvare
Fiind variabile independente, probabilitatea că toate să fie pozitive este egală cu produsul probabilităților că fiecare să fie pozitivă: \[P(X > 0 \cap Y > 0 \cap Z > 0) = P(X > 0) \cdot P(Y > 0) \cdot P(Z > 0)\]
Întrucât toate urmează aceeași distribuție, probabilitatea ca \(X\) să fie pozitivă este egală cu probabilitatea ca \(Y\) sau ca Z să fie pozitivă, așadar trebuie de fapt să calculăm o singură probabilitate, și apoi să o ridicăm la puterea 3.
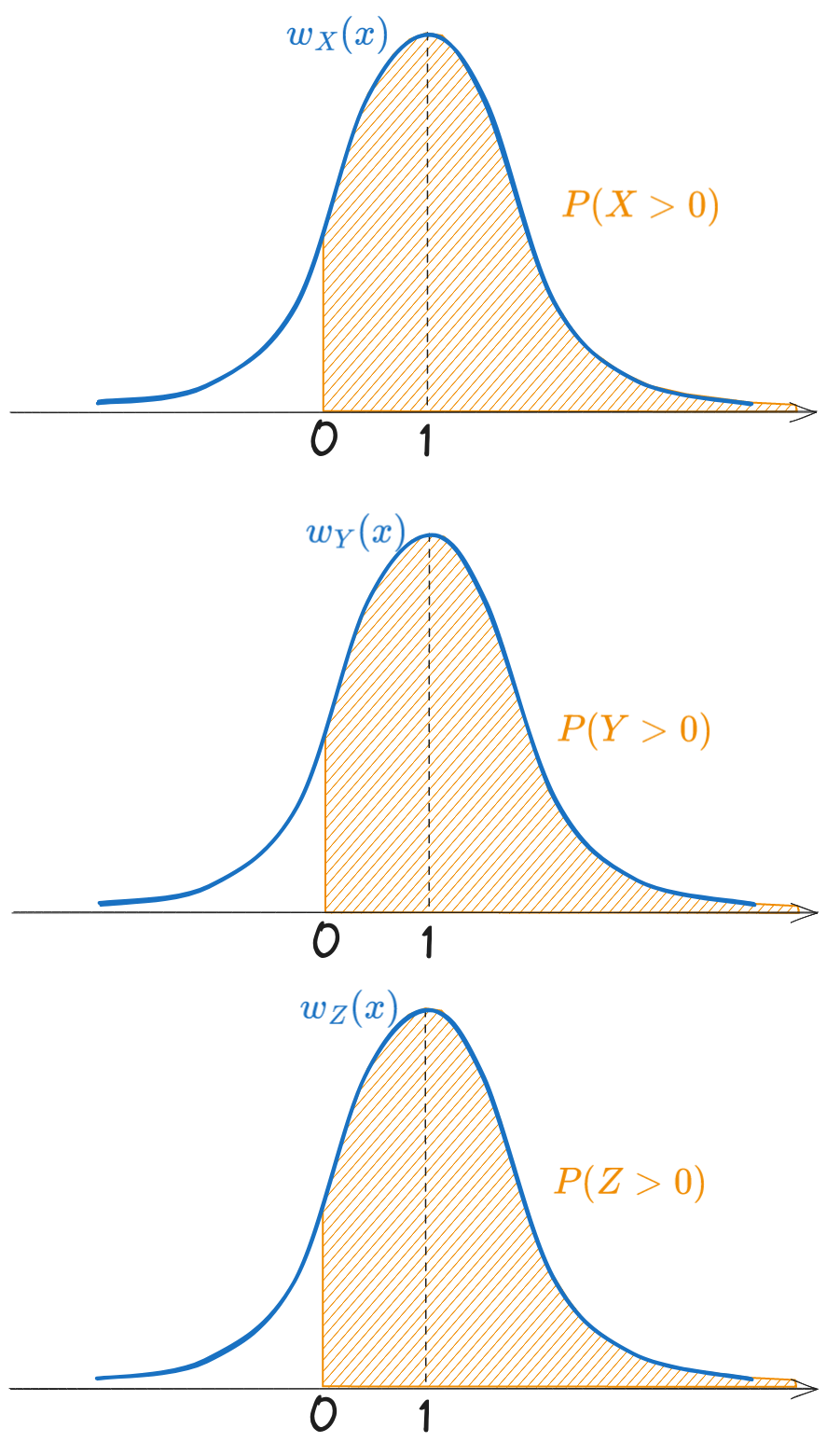
Avem: \[\begin{aligned} P(X > 0) &= (Y > 0) = P(Z > 0) = \int_{0}^{\infty} w_X(x) dx = F(\infty) - F(0) \\ &= 1 - \frac{1}{2} \left(1 + erf \left(\frac{0 - 1}{\sqrt{2}\cdot 1}\right)\right) \\ &= 1 - \frac{1}{2} \left(1 + erf \left(-\frac{1}{\sqrt{2}}\right)\right) \\ &= 0.841 \end{aligned}\]
Așadar, probabilitatea că toate să fie pozitive este: \[P(X > 0, Y > 0, Z > 0) = 0.841^3 = 0.595\]
8.6 Exercițiul 6
Fie 3 variabile aleatoare cu distribuțiile: \[ \begin{aligned} A &\sim \mathcal{N}\; \left(\mu=1, \sigma^2=3\right) \\ B &\sim \mathcal{N}\; \left(\mu=-4, \sigma^2=3\right) \\ C &\sim \mathcal{N}\; \left(\mu=5, \sigma^2=3\right) \end{aligned}\]
- a). Este mai probabil ca tripleta de valori (A, B, C) să ia valori în jurul lui (2, -6, 3) sau în jurul lui (-2, -3, 2)?
- b). Găsiți 3 valori pozitive \((x, y, z)\) pentru care probabilitatea ca (A, B, C) să aibă valori în jurul lui \((x,y,z)\) să fie egală cu probabilitatea de a avea valori în jurul lui (2, -6, 3)
Rezolvare
TODO