6 Algoritmi practici
În continuare, vom studia o serie de algoritmi practici, foarte utilizați atunci când distribuțiile datelor sunt necunoscute.
În analiza de până acum, am considerat că se cunosc întotdeauna parametrii matematici ai tuturor datelor:
- Se cunosc semnalele \(s_0(t) = ...\), \(s_1(t) = ...\)
- Se cunoaște zgomotul (gaussian, uniform etc.)
- Se cunosc distribuțiile condiționate \(w(r|H_0)\), \(w(r|H_1)\)
În aplicații reale, multe dintre acestea pot fi de fapt necunoscute, sau nedefinite.
Exemplu: recunoașterea feței unei persoane
- Identificarea persoanei A sau B bazată pe o imagine a feței
- Avem:
- 100 imagini ale persoanei A, în condiții diverse
- 100 imagini ale persoanei B, în condiții diverse
Să comparăm recunoașterea fețelor cu detecția semnalelor
- Aspecte comune:
- două ipoteze \(H_0\) (persoana A) și \(H_1\) (persoana B)
- un vector de eșantioane \(\vec{r}\) = imaginea pe baza căreia se face decizia
- se pot lua două decizii
- 4 scenarii: rejecție corectă, alarmă falsă, pierdere, detecție corectă
- Ce diferă? Nu există formule matematice
- nu există semnalele “originale” \(s_0(t) = ...\) și \(s_1(t)...\)
- (fețele persoanelor A și B nu pot fi exprimate matematic ca semnale)
- în schimb, avem multe exemple din fiecare distribuție
- 100 imagini ale lui A = exemple ale \(\vec{r}\) în ipoteza \(H_0\)
- 100 imagini ale lui B = exemple ale \(\vec{r}\) în ipoteza \(H_1\)
Terminologia folosită în domeniul învățării automate (machine learning):
Acest tip de problemă = problemă de clasificare a semnalelor
- se dă un vector de date, găsiți-i clasa
Clase de semnal = categoriile posibile ale semnalelor (ipotezele \(H_i\), persoanele A/B etc)
Set de antrenare = un set de semnale cunoscute inițial
- de ex. 100 de imagini ale fiecărei persoane
- setul de date va fi folosit în procesul de decizie
Setul de antrenare conține informațiile pe care le-ar conține distribuțiile condiționate \(w(r|H_0)\) și \(w(r|H_1)\)
- \(w(r|H_0)\) exprimă cum arată valorile lui \(r\) în ipoteza \(H_0\)
- \(w(r|H_1)\) exprimă cum arată valorile lui \(r\) în ipoteza \(H_1\)
- setul de antrenare exprimă același lucru, nu prin formule, dar prin multe exemple
Cum se face clasificarea în aceste condiții?
6.1 Algoritmul k-NN
6.1.1 Definiția algoritmului
Algoritmul k-Nearest Neighbours (k-NN) este descris mai jos.
Intrare:
- set de antrenare cu vectorii \(\vec{x}_1 ... \vec{x}_N\), din \(L\) clase posibile de semnal \(C_1\)…\(C_L\)
- clasele vectorilor de antrenare sunt cunoscute
- vector de test \(\vec{r}\) care trebuie clasificat
- parametrul \(k\)
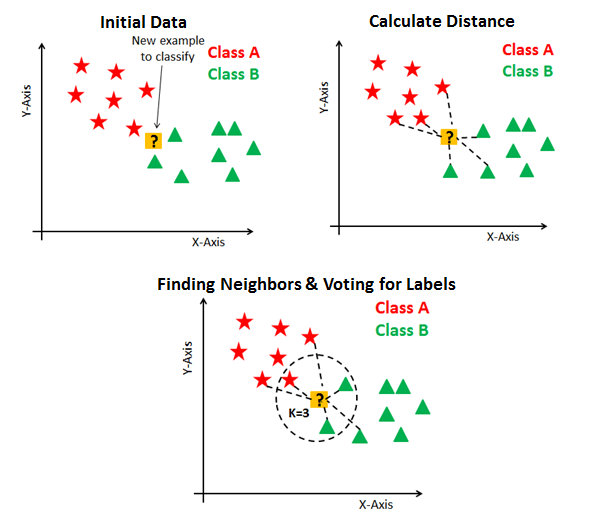
Se calculează distanța între \(\vec{r}\) și fiecare vector de antrenare \(\vec{x}_i\)
- se poate utiliza distanța Euclidiană, aceeași utilizată pentru detecția semnalelor din secțiunile precedente
Se aleg cei mai apropiați \(k\) vectori de \(\vec{r}\) (cei \(k\) “nearest neighbours”)
Se determină clasa lui \(\vec{r}\) = clasa majoritară între cei \(k\) cei mai apropiați vecini
- Ieșire: clasa vectorului \(\vec{r}\)
6.1.2 Relația între k-NN și decizia ML
Dacă setul de antrenare este foarte mare, algoritmul k-NN devine simular cu decizia pe baza criteriului ML, pentru că numărul de vectori situați într-o vecinătate a unui punct \(r\) este proporțional cu \(w(r|H_i)\). Așadar, dacă sunt mai mulți vecini din clasa A decât din clasa B, caz în care k_NN ia decizia A, e totuna cu a spune că \[w(r|H_A) > w(r|H_B)\] care este de fapt regula de decizie ML, tot în favoarea clasei A.
Exemplu: frunze și copaci, de povestit.
6.1.3 Discuții
Algoritmul k-NN este un algoritm de învățare supervizată, întrucât se cunosc clasele vectorilor din setul de antrenare.
Efectul lui \(k\) se reflectă în gradul de “netezire” a frontierei de decizie: - \(k\) mic: frontieră foarte cotită / “șifonată” / cu multe coturi - \(k\) mare: frontieră mai netedă
Cum se găsește o valoare optimă pentru \(k\)?. În general, doar prin încercări (“băbește”), pe baza unui mic set de date de test. Această metodă se numește “cross-validation”.
“Cross-validation” = folosirea unui mic set de test pentru a verifica care valoare a parametrului e mai bună
Acest set de date se numește set de “cross-validare”.
Practic, se alege \(k=1\), și se testează cu setul de “cross-validare” câți vectori sunt clasificați corect. Apoi se repetă pentru \(k=2, 3, ... max\). La final se alege valoarea lui \(k\) cu care s-au obținut rezultatele cele mai bune.
6.1.4 Evaluarea algoritmilor
- Cum se evaluează performanța algoritmului k-NN?
- Se folosește un set de date de testare, și se calculează procentajul vectorilor clasificați corect
- Setul de date pentru evaluarea finală trebuie să fie diferit de setul de “cross-validare”
- pentru evaluarea finală se folosesc date pe care algoritmul nu le-a mai utilizat niciodată
- Cum se împarte setul de date disponibile?
6.1.5 Seturi de date
- Presupunem că avem în total 200 imagini tip fețe, 100 imagini ale persoanei A și 100 ale lui B
- Setul de date total se împarte în:
- Set de antrenare
- vectorii care vor fi utilizați de algoritm
- cel mai numeros, aprox. 60% din datele totale
- de ex. 60 imagini ale persoanei A și 60 ale lui B
- Set de cross-validare
- utilizat pentru a testa algoritmul în vederea alegerii parametrilor optimi (\(k\))
- mai mic, aprox. 20% din date (de ex. 20 imagini ale lui of A și 20 ale lui B)
- Set de testare
- utilizat pentru evaluarea finală a algoritmului, cu valorile parametrilor fixate
- mai mic, aprox. 20% din date (de ex. 20 imagini ale lui of A și 20 ale lui B)
- Set de antrenare
6.2 Algoritmul k-Means
k-Means este un algoritm pentru clusterizarea datelor.
Prin clusterizare se înțelege operația de identificare a grupurilor de date apropiate între ele (clustere).
6.2.1 Definiția algoritmului
Algoritmul k-Means funcționează astfel:
- Intrare:
- set de antrenare cu vectorii \(\vec{x}_1 ... \vec{x}_N\)
- numărul de clase C
- Inițializare: centroizii C iau valori aleatoare \[\vec{c}_i \leftarrow \textrm{ valori aleatoare }\]
- Repetă
- Clasificare: se clasifică fiecare vector \(\vec{x}\) pe baza celui mai apropiat centroid: \[class{x} = \arg\min_i d(\vec{x}, \vec{c}_i), \forall \vec{x}\]
- Actualizare: se actualizează centroizii \(\vec{c}_i\) = media vectorilor \(\vec{x}\) din clasa \(i\) \[\vec{c}_i \leftarrow \textrm{ media vectorilor } \vec{x}, \forall \vec{x} \textrm{ din clasa } i\]
- Ieșire: centroizii \(\vec{c}_i\), clasele tuturor vectorilor de intrare \(\vec{x}_n\)
Pentru explicații video pe Youtube:
Urmăriți video-ul următor, de la 6:28 to 7:08
Urmăriți video-ul următor, de la 3:05 la final
6.2.2 Discuții
Algoritmul k-Means este un exemplu de algoritm de învățare nesupervizată.
Învățare nesupervizată = când nu se cunosc clasele semnalelor din setul de antrenare
Algoritmul k-Means poate să nu conveargă spre niște grupuri adecvate de date. Cu alte cuvinte, rezultate bune nu sunt garantate; rezultatele depind foarte mult de inițializarea aleatoare a centroizilor.
O soluție frecventă, în practică, este să rulăm algoritmul de mai multe ori, pentru a alege apoi cel mai bun rezultat. De asemenea, există în literatură și unele metode de inițializare optimizate (k-Means++)