4 Decizie cu un singur eșantion

4.1 Introducere

O problemă de decizie înseamnă, pe scurt, a decide între două alternative.

În contextul comunicațiilor, detecția semnalelor înseamnă a decide care semnal este prezent dintre două sau mai multe posibilități, în condițiile în care semnalul este afectat de zgomot aditiv (se adună la semnalul original)

Dificultatea este cauzată de zgomot, care ne poate “păcăli” în a lua o decizie greșită. Se pune așadar problema cum putem decide în mod robust, minimizând efectul zgomotului.

Pentru fixarea ideilor, prezentăm mai jos o schemă de principiu a unui sistem de comunicații..

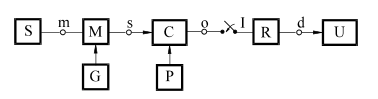
Figure 4.1: Schema bloc a unui sistem de comunicație

Elemente:

Sursa de informație: generează mesajele $a_n$
Generator: generează semnalele diferite $s_1(t)$,…$s_n(t)$
Modulator: transmite semnalul $s_n(t)$ aferent mesajului $a_n$
Canal: adaugă zgomot aleator
Eșantionare: ia eșantioane din semnalul $s_n(t)$
Receptor: decide ce mesaj $a_n$ s-a fost recepționat
Utilizator: primește mesajele recuperate

Aplicații:

Transmisii de date cu diverse modulații binare:
- nivele constante de tensiune (de ex. $s_n(t)$ = constant 0 sau 5V)
- modulație PSK (Phase Shift Keying): $s_n(t)$ = cosinus cu aceeași frecvență dar faze inițiale diferite
- modulație FSK (Frequency Shift Keying): $s_n(t)$ = cosinus cu frecvențe diferite
- modulație OFDM (Orthogonal Frequency Division Multiplexing): caz particular de FSK
Detecții radar

Se emite un semnal, iar în cazul unui obstacol, semnalul se reflectă înapoi. Receptorul așteaptă posibilele reflecții ale semnalului emis și decide:
- dacă nu este prezentă o reflecție, se decide că nu există nici un obiect
- dacă semnalul reflectat este prezent, se decide că există un obiect

Problema se poate generaliza în cazul mai multor semnale posibile.

Decizie se poate baza pe un singur eșantion, pe mai multe eșantioane, sau pe observarea întregului semnal continuu pentru un timp $T$, cazuri care vor fi tratate separat.

4.2 Decizie cu 1 eșantion

Vom analiza mai întâi cel mai simplu scenariu, când la recepție se ia un singur eșantion din semnalul recepționat, și se decide pe baza sa.

Vom porni de la cea mai simplu exemplu posibil.

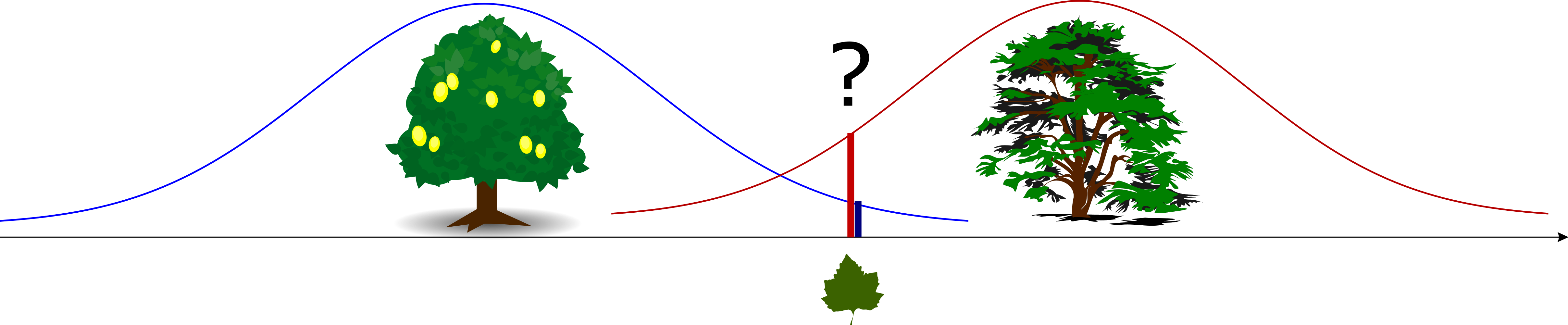
Să prespunem că se transmite un bit, 0 logic sau 1 logic, folosind două nivele de tensiune constante. De exemplu, pentru 0 logic se poate transmite semnalul \[s_0(t) = 0\] iar pentru 1 logic se poate transmite semnalul \[s_1(t) = 5\]

Pe canalul de transmisie se suprapune zgomot. La recepție se ia un singur eșantion $r$, și valoarea sa este $3.5$.

Ce decizie luăm? Am recepționat un 0 sau un 1 logic?

Problema se poate formula mai general astfel:

Există două mesaje posibile $a_0$ și $a_1$ (0 logic sau 1 logic)
Se transmite un semnal $s(t)$, care poate fi $s(t) = s_0(t)$, a transmite $a_0$, sau $s(t) = s_1(t)$, pentru a transmite $a_1$
Peste semnal se suprapune zgomotul $n(t)$
La recepție se primește un semnal cu zgomot, $r(t) = s(t) + n(t)$
Problema deciziei: pe baza $r(t)$, care semnal a fost cel transmis?

Vom introduce următoarea terminologie, cu notațiile aferente.

Există două ipoteze, notate $H_0$ și $H_1$:

$H_0$: semnalul adevărat este $s(t) = s_0(t)$
$H_1$: semnalul adevărat este $s(t) = s_1(t)$

Receptorul poate lua una din două decizii, notate $D_0$ și $D_1$:

$D_0$: receptorul decide că semnalul corect este $s(t) = s_0(t)$
$D_1$: receptorul decide că semnalul corect este $s(t) = s_1(t)$

Există 4 situații posibile:

Rejecție corectă: ipoteza corectă este $H_0$, decizia este $D_0$
- Probabilitatea este $P_r = P(D_0 \cap H_0)$
- Se mai numește si “True Negative”
Alarmă falsă: ipoteza corectă este $H_0$, decizia este $D_1$
- Probabilitatea este $P_{af} = P(D_1 \cap H_0)$
- Se mai numește și “False Positive”
Pierdere: ipoteza corectă este $H_1$, decizia este $D_0$
- Probabilitatea este $P_p = P(D_0 \cap H_1)$
- Se mai numește și “False Negative”
Detecție corectă: ipoteza corectă este $H_1$, decizia este $D_1$
- Probabilitatea este $P_d = P(D_1 \cap H_1)$
- Se mai numește și “True Positive”

Terminologia folosită are la origine aplicațiile radar, în care un semnal se emite de către sursă, iar semnalul recepționat poate conține, sau nu, o posibilă reflecție din partea unei ținte. Reflecția e puternic afectată de zgomot, ceea ce ne poate induce în eroare:

“alarmă falsă” înseamnă ca nu există un obiect în realitate (ipoteza $H_0$), dar decizia este greșită și considră că există ($D_1$) nu există semnal reflectat (doar zgomot)
“pierdere” (“miss”, lb.eng.) înseamnă că există un obiect în realitate (ipoteza $H_1$), dar decizia este că nu e nimic acolo ($D_0$)

În general se consideră zgomot aditiv, alb, staționar suprapus peste semnalul original

aditiv = zgomotul se adună cu semnalul
alb = eșantioane distincte sunt necorelate
staționar = are aceleași proprietăți statistice la orice moment de timp

Semnalul de zgomot $n(t)$ este necunoscut, dar este o realizare a unui proces aleator, pentru care se cunoaște doar distribuția.

La recepție se primește semnalul $r(t) = s(t) + n(t)$, unde:

$s(t)$ = semnalul original, fie $s_0(t)$, fie $s_1(t)$
$n(t)$ = semnalul de zgomot necunoscut

Din semnalul recepționat se ia un eșantion la momentul $t_0, adică: \[r(t_0) = s(t_0) + n(t_0)\] unde $s(t_0)$ = fie $s_0(t_0)$, fie $s_1(t_0)$, iar $n(t_0)$ este un eșantion de valoare necunoscută din semnalul de zgomot.

Eșantionul $n(t_0)$ este o variabilă aleatoare, fiind un eșantion de zgomot (un eșantion dintr-un proces aleator)

Așadar valoarea $r(t_0) = s(t_0) + n(t_0)$ este suma dintre o constantă și o variabilă aleatoare, ceea ce înseamnă ce este este de asemenea o variabilă aleatoare, având aceeași distribuție ca eșantionaul de zgomot, dar translată cu valoarea constantei.

Exemplu

Se transmite un semnal $s(t) = 2 \cos(2\pi \cdot 1000 \cdot t)$, peste care se suprapune un zgomot gaussian $n(t)$ cu distribuția $\mathcal{N}(\mu=0, \sigma^2=0.5)$. \[r(t) = s(t) + n(t)\]

La recepție se ia un eșantion la momentul $t_0 = 1$. Atunci eșantionul are valoarea \[r = r(1) = s(1) + n(1) = 2 \cos(2\pi \cdot 1000 \cdot 1) + n(1) = 2 + n(1)\]

Întrucât $n(1)$ are distribuția $\mathcal{N}(\mu=0, \sigma^2=0.5)$, atunci $r$ are distribuția $\mathcal{N}(\mu=2, \sigma^2=0.5)$.

4.3 Funcții de plauzibilitate

Să presupunem că distribuția unui eșantion de zgomot este $w(x)$.

În ipoteza $H_0$, adică dacă semnalul adevărat era $s_0(t)$, atunci eșantionul $r$ are distribuția: \[w(r|H_0) = s_0(t_0) + w(x) = w(x)\textrm{ translat cu } s_0(t_0)\]
În ipoteza $H_1$, adică dacă semnalul adevărat era $s_1(t)$, atunci eșantionul $r$ are distribuția: \[w(r|H_1) = s_1(t_0) + w(x) = w(x)\textrm{ translat cu } s_1(t_0)\]

Cele două distribuții vor fi numite distribuțiile condiționate sau funcțiile de plauzilibilate

Problema deciziei se poate formula astfel:

“Care dintre cele două distribuții, $w(r|H_0)$ și $w(r|H_0)$, este mai probabil să fi generat valoarea $r$ a eșantionului observat la recepție?”

Exercițiu

Un semnal constant $s(t)$ poate avea două valori posibile, 0 sau 4. Semnalul este afectat de zgomot $\mathcal{N}(\mu=0, \sigma^2 = 2)$. Care e distribuția unui eșantion $r$, în ambele ipoteze?

Se definește plauzibilitatea unei ipoteze $H_i$ pe baza observației $r$ ca fiind: \[L(H_i | r) = w(r | H_i)\] adică valoarea distribuției condiționate de ipoteza $H_i$, evaluată la valoarea $r$ a eșantionului observat.

În cazul nostru, plauzibilitatea ipotezei $H_0$ este: \[L(H_0 | r) = w(r | H_0)\] și a ipotezei $H_1$ este: \[L(H_1 | r) = w(r | H_1)\]

4.4 Criteriul Plauzibilității Maxime (Maximum Likelihood)

Dacă trebuie să decidem care dintre cele două ipoteze, $H_0$ sau $H_1$, este “responsabilă” pentru producerea valorii $r$, o alegere naturală este ipoteza cu plauzibilitate mai mare.

Criteriul plauzibilității maxime (“Maximum Likelihood”, ML): \[\frac{L(H_1 | r)}{L(H_0 | r)} = \frac{w(r|H_1)}{w(r|H_0)} \grtlessH 1\]

Fracția $\frac{w(r|H_1)}{w(r|H_0)}$ poartă numele de raport de plauzibilitate. În criteriul ML, raportul de plauzibilitate se compară cu 1:

dacă este supraunitar, se ia decizia $D_1$ ($w(r|H_1)$ e mai mare)
dacă este subunitar, se ia decizia $D_0$ ($w(r|H_0)$ e mai mare)
dacă este egal cu 1, avem o indecizie (plauzibilitățile sunt egale)

Practic, decizia se ia alegând ipoteza cu cea mai mare plauzibilitate pentru valoarea $r$, adică se alege valoarea maximă dintre $w(r(t_0)|H_0)$ și $w(r(t_0) | H_1)$.

Exemplu: Frunze

Din care copac a căzut frunza?

Exercițiu

Care e decizia luată cu criteriul ML, pentru un eșantion $r=1.6$?

Se schițează a celor două distribuții condiționate $w(r|H_0)$ și $w(r|H_1)$
Care funcție e mai mare în dreptul lui $r = 1.6$?

Discuție: ce decizie se ia pentru diferite valori ale lui $r$

Discuție: care este pragul $T$ pentru decizii?

4.4.1 Praguri și regiuni de decizie

Punctele în care cele două distribuții condiționate $w(r|H_0)$ și $w(r|H_1)$ se intersectează determină niște praguri de decizie. Alegerea valorii celei mai apropiate pentru o decizie, echivalează, defapt, cu compararea lui $T$ cu aceste praguri.

Regiunile de decizie reprezintă intervalul de valori ale eșantionului $r$ pentru care se ia o anumită decizie

Regiunea de decizie $R_0$ = intervalul de valori ale lui $r$ care conduc la decizia $D_0$
Regiunea de decizie $R_1$ = intervalul de valori ale lui $r$ care conduc la decizia $D_1$

Regiunile de decizie acoperă întreg domeniul de valori ale lui $r$ (toată axa reală), exceptând punctele sau regiunile de indecizie, unde nu se poate lua nici decizie $D_0$ nici $D_1$.

4.4.2 Probabilități condiționate

Probabilitățile condiționate ale celor 4 rezultate posibile ale unei decizii binare se definesc în felul următor.

Probabilitatea condiționată a rejecției corecte reprezintă probabilitatea de a lua decizia $D_0$ când ipoteza este $H_0$, și se calculează ca probabilitatea lui $r$ să fie în $R_0$, calculată pe distribuția $w(r|H_0)$ \[P(D_0 | H_0) = \int_{R_0} w(r|H_0) dx\]

Probabilitatea condiționată a alarmei false reprezintă probabilitatea de a lua decizia $D_1$ când ipoteza corectă este $H_0$, și se calculează ca probabilitatea ca $r$ să fie în $R_1$, calculată pe distribuția $w(r|H_0)$ \[P(D_1 | H_0) = \int_{R_1} w(r|H_0) dx\]

Probabilitatea condiționată de pierdere reprezintă probabilitatea de a lua decizia $D_0$ când ipoteza corectă este $H_1$, și se calculează ca probabilitatea ca $r$ să fie în $R_0$, calculată pe distribuția $w(r|H_1)$ \[P(D_0 | H_1) = \int_{R_0} w(r|H_1) dx\]

Probabilitatea condiționată a detecției corecte reprezintă probabilitatea de a lua decizia $D_1$ când ipoteza este $H_1$, și se calculează ca probabilitatea ca $r$ să fie în $R_1$, calculată pe distribuția $w(r|H_1)$ \[P(D_1 | H_1) = \int_{R_1} w(r|H_1) dx\]

Cele patru probabilități condiționate corespund celor patru arii din fig.xxx, determinate ce cele două distribuții condiționate și cele două regiuni de decizie.

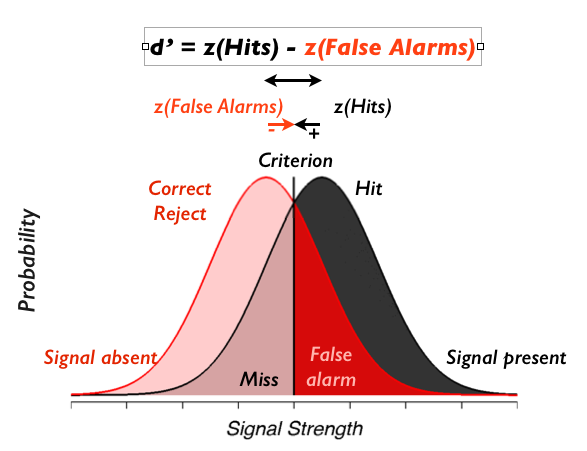
Ignorați textul, contează zonele colorate
[sursa: hhttp://gru.stanford.edu/doku.php/tutorials/sdt]*

Între cele patru probabilități există următoarele relații:

\[P(D_0 | H_0) + P(D_1 | H_0) = 1\] (rejecție corectă + alarmă falsă) \[P(D_0 | H_1) + P(D_1 | H_1) = 1\] (pierdere + detecție corectă)

Exercițiu

Demonstrați cele două relații de mai sus.

Exercițiu

Un semnal constant poate avea două valori posibile, $0$ sau $5$. Semnalul este afectat de zgomot gaussian $\mathcal{N}\;(\mu=0, \sigma^2=2)$. Receptorul decide pe baza criteriului plauzibilității maxime, folosind un singur eșantion din semnal.

Calculați probabilitatea condiționată a alarmei false
Calculați probabilitatea condiționată de pierdere
Dacă $P(H_0) = \frac{1}{3}$ și $P(H_1) = \frac{2}{3}$, calculați probabilitatea rejecției corecte și a detecției corecte (nu cele condiționate)

4.4.3 Optimalitatea criteriului ML

Teoremă: optimalitatea criteriului ML

Criteriul ML minimizează suma probabilităților condiționate de eroare, $P(D_1 | H_0) + P(D_0 | H_1)$.

Demonstrație:

Informal: de pe figura precedentă, dacă pragul $T$ se deplasează fie la dreapta fie la stânga, suma celor două arii hașurate (probabilități) pentru alarmă falsă + pierdere crește.

TODO: demonstrație riguroasă

Teorema ne spune că criteriul ML de decizie ne asigură cea mai mică probabilitate (condiționată) de a greși.

4.5 Criteriul probabilității minime de eroare (Minimum Probability of Error, MPE)

Criteriul ML compară doar distribuțiile condiționate ale eșantionului observat, ceea ce înseamnă că nu ia în calcul și probabilitatea inițială celor două ipoteze, $P(H_0)$ și $P(H_1)$. Dacă se consideră si acestea, ajungem la un alt criteriu de decizie, intitulat criteriul probabiității minime de eroare.

Criteriul probabilității minime de eroare (Minimum Probabilityof Error, MPE): \[\frac{P(H_1) \cdot w(r | H_1)}{P(H_0) \cdot w(r | H_0)} \grtlessH 1\]

Criteriul poate fi rescris tot ca o comparație a raportului de plauzibilitate, de data aceasta comparat cu raportul celor două probabilități ale ipotezelor. \[\frac{w(r | H_1)}{w(r | H_0)} \grtlessH \frac{P(H_0)}{P(H_1)}\]

Criteriul MPE este o generalizare a criteriului ML, care ia în calcul și probabilitățile $P(H_0)$ și $P(H_1)$. Criteriul ML poate fi considerat un caz particular al MPE pentru cazul uner probabilități egale ale ipotezelor, $P(H_0) = P(H_1) = \frac{1}{2}$.

Teoremă: Optimalitatea criteriului MPE

Criteriul MPE minimizează probabilitatea totală de eroare: \[P_e = P_{af} + P_p = P(D_1 \cap H_0) + P(D_0 \cap H_1)\]

Aceste probabiiltăți nu sunt probabilitățile condiționate, ca la criteriul ML, ci sunt cele care includ $P(H_i)$ (probabilități necondiționate).

Demonstrație:

Criteriul MPE înseamnă, de fapt, decizia în felul următor:

Când $w(r|H_1) \cdot P(H_1) - w(r|H_0) \cdot P(H_0) < 0$ se ia decizia $D_0$
Când $w(r|H_1) \cdot P(H_1) - w(r|H_0) \cdot P(H_0) > 0$ se ia decizia $D_1$

Probabilitatea unei alarme false este: \[\begin{split} P(D_1 \cap H_0) =& P(D_1 | H_0) \cdot P(H_0)\\ =& \int_{R_1} w(r | H_0) dx \cdot P(H_0)\\ =& (1 - \int_{R_0} w(r | H_0) dx \cdot P(H_0) \end{split}\]

Probabilitatea de pierdere este: \[\begin{split} P(D_0 \cap H_1) =& P(D_0 | H_1) \cdot P(H_1)\\ =& \int_{R_0} w(r | H_1) dx \cdot P(H_1) \end{split}\]

Suma lor reprezintă probabilitatea totală a erorilor; \[P_e = P(H_0) + \int_{R_0} [w(r|H_1) \cdot P(H_1) - w(r|H_0) \cdot P(H_0)] dx\]

Conform criteriului MPE, regiunea de decizie $R_0$ cuprinde toate valorile pentru care \[w(r|H_1) \cdot P(H_1) - w(r|H_0) \cdot P(H_0) < 0,\] adică de fapt întreaga zonă în care integrala de mai sus este negativă. Acest lucru garantează valoarea minimă a integralei, deci valoarea minimă a $P_e$ (termenul $P(H_0)$ fiind constant).

Exercitiu: 0/5, prag la 2.5, numar de erori.

4.6 Criteriul riscului minim (Minimum Risk, MR)

Există situații în care ne afectează mai mult un anume tip de erori (de ex. alarme false) decât celelalte (pierderi). Criteriul MPE tratează toate erorile la fel, ceea ce nu ajută în aceste cazuri.

Pentru a descrie un astfel de scenariu, se atribuie un cost fiecărui scenariu, $C_{ij}$ fiind costul deciziei $D_i$ când ipoteza adevărată este $H_j$, ideaa fiind de a minimiza costul mediu.

$C_{00}$ = costul unei rejecții corecte
$C_{10}$ = costul unei alarme false
$C_{01}$ = costul unei pierderi
$C_{11}$ = costul unei detecții corecte

Vrem să minimizăm costul mediu, numit și risc, calculat astfel: \[R = C_{00} P(D_0 \cap H_0) + C_{10} P(D_1 \cap H_0) + C_{01} P(D_0 \cap H_1) + C_{11} P(D_1 \cap H_1)\]

Ideea de “costuri” și minimizare a costului mediu este frecvent întâlnită în literatura de specialitate. De exemplu, în codarea informației, “costul” unui mesaj este lungimea cuvântului de cod asociat, iar minimizarea costului mediu înseamnă minimizarea lungimii medii.

Minimizarea riscului $R$ conduce la următoarea regulă de decizie.

Criteriul riscului minim (Minimum Risk, MR): \[\frac{w(r|H_1)}{w(r|H_0)} \grtlessH \frac{(C_{10}-C_{00})p(H_0)}{(C_{01}-C_{11})p(H_1)}\]

Se observă că criteriul MR este o generalizare a criteriului MPE, la rândul lui o generalizare a ML, și se exprimă tot pe baza unui raport de plauzibilitate.

Atât probabilitățile cât și costurile pot influența decizia în favoarea uneia sau alteia dintre ipoteze

Ca și caz particular, dacă $C_{10}-C_{00} = C_{01}-C_{11}$, atunci MR se reduce la criteriul MPE.

Teoremă: Optimalitatea criteriului MR

Criteriul MR definit mai sus asigură valoarea minimă a riscului $R$.

Demonstrație

La tablă.

4.7 Forma generală a criteriilor ML, MPE și MR

Criteriile ML, MPE și MR au toate forma următoare: \[\frac{w(r|H_1)}{w(r|H_0)} \grtlessH K,\] unde $K$ depinde de criteriul folosit:

pentru ML: $K=1$
pentru MPE: $K=\frac{P(H_0)}{P(H_1)}$
pentru MR: $K=\frac{(C_{10}-C_{00})p(H_0)}{(C_{01}-C_{11})p(H_1)}$

4.8 Criteriile ML, MPE și MR pentru zgomot gaussian

Considerăm un caz foarte des întâlnit în practică, acela în care zgomotul are o distribuție normală cu medie 0, $\mathcal{N}(0,\sigma^2)$. Cu alte cuvinte, avem un zgomot tip AWGN.

Considerând forma comună a tuturor celor trei criterii, expresia devine): \[\frac{w(r|H_1)}{w(r|H_0)} = \frac{e^{-\frac{(r-s_1(t_0))^2}{2\sigma^2}}}{e^{-\frac{(r-s_0(r_0))^2}{2\sigma^2}}} \grtlessH K\]

Aplicăm logaritmul natural acestei relații. Întrucât orice logaritm este o funcție monoton crescătoare, el nu schimbă rezultatul unei comparații (dacă $A < B$, atunci $\log(A) < \log(B)$). Prin urmare, deciziile nu vor fi afectate. Aplicarea logaritmului natural la ambii termeni ai relației conduce la: \[-(r-s_1(t_0))^2 + (r-s_0(t_0))^2 \grtlessH \ln(K)\] care este echivalent cu: \[(r-s_0(t_0))^2 \grtlessH (r - s_1(t_0))^2 + \ln(K).\]

Relația de mai sus se poate interpreta ca o comparația a distanțelor geometrice. Termenul $(r-s_0(t_0)^2$ este pătratul distanței goemetrice, pe axa numerelor reale, dintre $r$ și $s_0(t_0)$, iar $(r-s_1(t_0))^2$ pătratul distanței de la $r$ la $s_1(t_0)$. Așadar, putem spune că se compară pătratul a două distanțe, cu un termen suplimentar $\ln(K)$ care influențează balanța în favoarea uneia sau alteia dintre decizii (în funcție de probabiități și/sau costuri).

Pentru criteriul ML, $K=1$, $\ln(K) = 0$ și relația se reduce chiar la alegerea distanței minime dintre $r(t_0)$ și $s_1(t_0)$, respectiv $s_0(t_0)$.

Din acest motiv, un sistem receptor care folosește criteriul de decizie ML se mai numește receptor de distanță minimă (“minimum distance receiver”)

Luarea unei decizii pe baza distenței minime se mai numește și principiul celui mai apropiat vecin (“nearest neighbor”), și este un principiu foarte general, foarte des întâlnit in literatura de specialitate, sub diverse alte forme.

Relația poate fi prelucrată în continuare. Prin desfacerea parantezelor se ajunge la: \[r \grtlessH \frac{s_0(t_0) + s_1(t_0)}{2} + \frac{\sigma^2}{s_1(t_0) - s_0(t_0)} \cdot\ln K\]

Termenul din dreapta definește valoarea de prag T. Putem spune, așadar, că decizia se ia comparându-l pe $r$ cu pragul $T$.

4.9 Alte considerații

4.9.1 Probabilitate vs plauzibilitate

Există o distincție subtilă între termenii “probabilitate” și “plauzibilitate”. Să considerăm distribuția condiționată $w(r | H_i)$ de la exemplul anterior:

\[\frac{1}{\sigma \sqrt{2 \pi}}e^{-\frac{(r - s_i(t_0))^2}{2\sigma^2}}\]

Care este necunoscuta în această expresie? În general, necunoscuta este $r$, dar în cazul problemei noastre de deciziei $r$ este cunoscut, și necunoscuta este de fapt $i$, 0 sau 1, care duce la valoarea maximă a expresiei.

În general, pentru aceeași expresie matematică a funcției de distribuție, dacă se cunosc parametrii statistici (de ex. $\mu$, $\sigma$, $H_i$) și necunoscuta este valoarea însăși (de ex. $r$, $x$) atunci funcția o interpretăm ca densitatea de probabilitate.

În situațiile, însă, în care că se cunoaște valoarea însăși (de ex. $r$, $x$) și necunoscuta este un parametru statistic (de ex. $\mu$, $\sigma$, $i$), atunci denumim funcția funcție de plauzibilitate. Acest lucru explică diferența subtilă dintre cei doi termeni, probabilitate și plauzibilitate, care în limbajul comun sunt practic sinonimi.

4.9.2 Generalizări

Problema de decizie analizată până acum se poate generaliza în mai multe moduri.

Dacă zgomotul are altă distribuție?
- Se schițează distribuțiile condiționate
- Se evaluează pentru $r = r(t_0)$
- Criteriul ML = se alege cea mai mare funcție $w(r|H_i)$ în punctul $r$ dat
Regiunile de decizie sunt date de punctele de intersecție ale distribuțiilor condiționate Pot fi mai multe intersectări, în general, deci mai multe praguri.
Dacă zgomotul are distribuție diferită în ipoteza $H_0$ față de ipoteza $H_1$?

În mod similar:
- Se schițează distribuțiile condiționate
- Se evaluează pentru $r = r(t_0)$
- Criteriul ML = se alege cea mai înaltă funcție $w(r|H_i)$ în punctul $r$ dat
Dacă cele două semnale $s_0(t)$ și $s_1(t)$ sunt constante / nu sunt constante?
- Nu contează forma semnalelor
- Tot ce contează sunt valorile celor două semnale la momentul de eșantionare $t_0$:
  - $s_0(t_0)$
  - $s_1(t_0)$
Dacă avem mai mult de 2 ipoteze?
- Se extinde raționamentul la $n$ ipoteze
- Avem $n$ semnale posibile $s_0(t)$, … $s_{n-1}(t)$
- Avem $n$ valori diferite $s_0(t_0)$, … $s_{n-1}(t_0)$
- Avem $n$ distribuții condiționate $w(r|H_i)$
- Se alege distribuția $w(r|H_i)$ cea mai înaltă pentru $r = r(t_0)$ dat
Dacă se iau mai multe eșantioane din semnale?
- Va fi tratat separat într-un subcapitol ulterior

Exercițiu

Fie decizia între două semnale constante: $s_0(t) = -5$ și $s_1(t)=5$. Semnalele sunt afectate de zgomot alb cu distribuție gaussiană $\mathcal{N}(0, \sigma^2=1)$ Receptorul ia un singur eșantion cu valoarea $r$.

Să se găsească regiunile de decizie conform criteriului MPE
Calculați probabilitatea alarmei false și probabilitatea de pierdere
Repetați a) și b) dacă $s_1(t)$ este afectat de zgomot uniform $\mathcal{U}[-4,4]$?

Exercițiu

Un sistem airbag detectează un accident prin eșantionarea semnalului de la un senzor cu 2 valori posibile: $s_0(t) = 0$ (OK) sau $s_1(t) = 5$ (accident).

Semnalul este afectat de zgomot gaussian $\mathcal{N}\;(\mu=0, \sigma^2=1)$.

Se ia un singur eșantion din semnal.

Costurile scenariilor sunt: $C_{00} = 0$, $C_{01} = 100$, $C_{10} = 10$, $C_{11} = -100$

Găsiți regiunile de decizie $R_0$ și $R_1$.

4.10 Criteriul Neyman-Pearson

Criteriul Neyman-Pearson:

Se aleg regiunile de decizie pentru a maximiza probabilitatea de detecție $P(D_1 \cap H_1)$, păstrând probabilitatea alarmei false sub o limită fixată $P(D_1 \cap H_0) \leq \lambda$.

Acesta este un criteriu mai general decât toate cele de până acum. Se poate arăta ca criteriile ML, MPE și MR sunt cazuri particulare ale Neyman-Pearson, pentru diverse valori ale $\lambda$.

Exercițiu

O sursă de informație produce două mesaje cu probabilitățile $p(a_0) = \frac{2}{3}$ și $p(a_1) = \frac{1}{3}$.

Mesajele sunt codate ca semnale constante cu valorile $-5$ ($a_0$) și $5$ ($a_1$).

Semnalele sunt afectate de zgomot alb cu distribuție uniformă $U [-5,5]$.

Receptorul ia un singur eșantion $r$.

Găsiți regiunile de decizie conform criteriului Neymar-Pearson, pentru $P_{fa} \leq 10^{-2}$
Care este probabilitatea de detecție corectă?

4.11 Metode de evaluare a rezultatelor

Cum se evaluează o problemă de decizie?

De exemplu, fie două problemă de decize binară:

Una în care avem $s_0(t) = 0$, $s_1(t) = 10$, și zgomot gaussian $\mathcal{N}(\mu=0, \sigma^2 = 4)$.
O altă în care $s_0(t) = 10$, $s_1(t) = 16$, și zgomot uniform $\mathcal{U}[-8, 8]$

Care dintre cele două probleme e mai dificilă? Cu alte cuvinte, în care vom obține rezultate mai slabe?

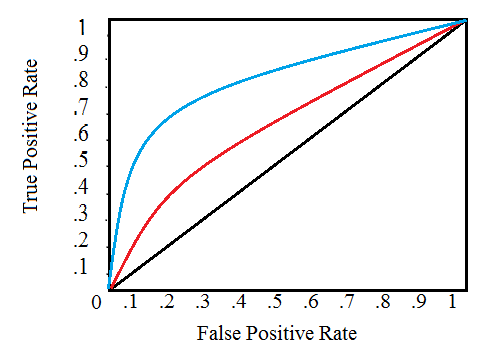
4.11.1 Caracteristica de operare a receptorului (ROC)

Performanța unui receptor poate fi ilustrată cu un grafic numit “Caracteristica de operare a receptorului” (“Receiver Operating Characteristic”, ROC)

Acesta reprezintă graficul probabilității $P_{dc} = P(D_1 | H_1)$ în funcție de probabilitatea $P_{af} = P(D_1 | H_0)$, pentru diferite praguri T. Fiecare punct de pe curbă corespunde unei valori a lui $T$.

[sursa: http://www.statisticshowto.com/receiver-operating-characteristic-roc-curve/]

Graficul ne arată că există întotdeauna un compromis între $P_d$ (bun) și $P_{fa}$ (rău). Creșterea $P_d$ implică și creșterea $P_{fa}$, și vice-versa.

O măsură a performanței globale a unui astfel de sistem este Area Under the Curve (AUC) a curbei ROC, care reprezintă, după cum îi spune și numele, aria totală de sub curba graficului. Aceasta valoare, cuprinsă între 0 și 1, este o valoare globală care caracterizează întregul sistem, indiferent de alegerea unui prag sau a altuia, deci indiferent de utilizarea unui criteriu sau al altuia.

Un AUC=1 înseamnă un sistem perfect, în care este posibil să obținem $P_d = 1$ și simultan $P_{fa} = 0$. În practică, desigur, se obțin valori mai mici decât 1.

Așadar, două situații diferite (două semnale diferite, algoritmi etc) se pot compara prin afișarea ROC si compararea AUC-urilor asociate

4.11.2 Caracteristica Precision vs Recall

Un grafic echivalent este cel de tip “Precision vs Recall”, întâlnit îndeosebi în literatura de specialitate din domeniul învățării automate (“machine learning”).

Cei doi termeni se definesc astfel:

Precision = $\frac{P(D_1 \cap H_1)}{P(D_1 \cap H_1) + P(D_1 \cap H_0)} = \frac{\textrm{True Positives}}{\textrm{True Positives + False Positives}}$

Recall = $\frac{P(D_1 \cap H_1)}{P(D_1 \cap H_1) + P(D_0 \cap H_1)} = P(D_1 | H_1) = \frac{\textrm{True Positives}}{\textrm{True Positives + False Negatives}}$

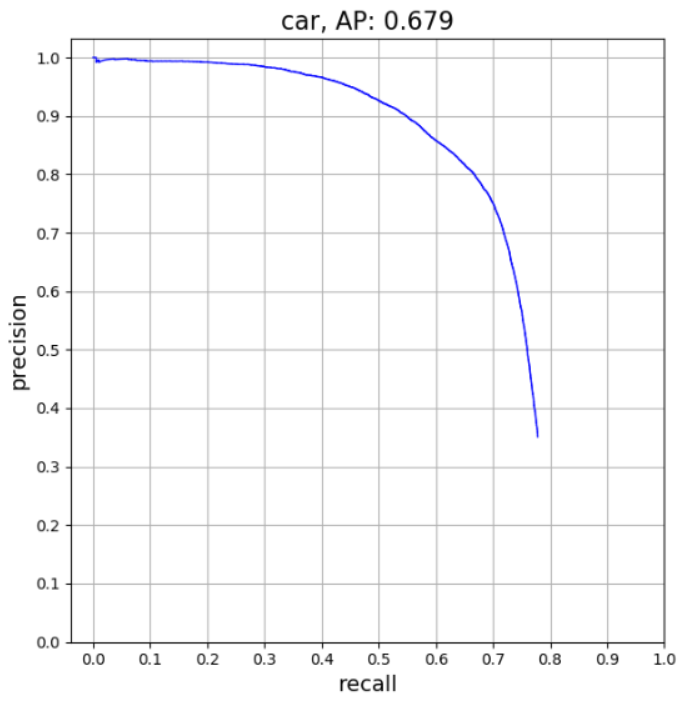
Curba Precision vs Recall dintr-o aplicație practică

Aplicația pentru care este obținut graficul precedent:

Detecția mașinilor cu metode de inteligență artificială

4.11.3 Raportul Semnal-Zgomot

Raportul semnal zgomot (SNR) al unui sistem se definește ca \[SNR = \frac{\text{puterea semnalului util}}{\text{puterea zgomotului}}\]

Performanțele oricărei probleme de decizie depind în mod fundamental de raportul semnal-zgomot al sistemului.

SNR mare: performanță bună
SNR mic: performanță slabă

De exemplu, să analizăm cum se pot îmbunătăți performanțele deciziei în situația din Fig.xxx. Aceasta se poate obține în două moduri:

Creșterea diferenței dintre $s_0(t)$ și $s_1(t)$, ceea ce înseamnă creșterea amplitudinilor, deci crește puterea semnalelor;
Scăderea zgomotului, adică scade puterea zgomotului.

Ambele soluții înseamnă, de fapt, creșterea raportului semnal zgomot.

Exemplu: Performanțele detecției în zgomot alb gaussian

Considerăm probabilități egale $P(H_0) = P(H_1) = \frac{1}{2}$.

Deciziile se iau pe baza raportului de plauzibilitate \[\frac{w(r|H_1)}{w(r|H_0)} \grtlessH K\]

Probabilitatea detecției corecte este \[\begin{split} P_d =& P(D_1 | H_1)\\ =& \int_{T}^{\infty} w(r | H_1) \\ =& (F(\infty) - F(T)) \\ =& \frac{1}{2} \left( 1 - erf \left( \frac{T - s_1(t_0)}{\sqrt{2}\sigma} \right) \right) \\ =& Q \left( \frac{T - s_1(t_0)}{\sqrt{2}\sigma} \right) \\ \end{split}\]

Probabilitatea alarmei false este \[\begin{split} P_{fa} =& P(D_1 | H_0) \\ =& \int_{T}^{\infty} w(r | H_0) \\ =& (F(\infty) - F(T)) \\ =& \frac{1}{2} \left( 1 - erf \left( \frac{T - s_0(t_0)}{\sqrt{2}\sigma} \right) \right) \\ =& Q \left( \frac{T - s_0(t_0)}{\sqrt{2}\sigma} \right) \\ \end{split}\]

Rezultă $\frac{T - s_0(t_0)}{\sqrt{2}\sigma} = Q^{-1} \left( P_{fa}\right)$,

și: $\frac{T - s_1(t_0)}{\sqrt{2}\sigma} = Q^{-1} \left( P_{fa}\right) + \frac{s_0(t_0) - s_1(t_0)}{\sqrt{2}\sigma}$

Înlocuind în $P_d$, obținem:

\[P_d = Q \left( \underbrace{Q^{-1} \left(P_{fa}\right)}_{constant} + \frac{s_0(t_0) - s_1(t_0)}{\sqrt{2}\sigma} \right)\]

Fie un scenariu simplu:

$s_0(t_0) = 0$
$s_1(t_0) = A = constant$

Obținem: \[P_d = Q \left( \underbrace{Q^{-1} \left(P_{fa}\right)}_{constant} - \frac{A}{\sqrt{2}\sigma} \right)\]

[sursa: Fundamentals of Statistical Signal Processing, Steven Kay]

4.12 Alte aplicații ale teoriei deciziei

Aceste criterii de decizie se pot utiliza și în alte aplicații, dintre cele mai generale, nu doar pentru a decide între semnale.

Esența matematică a problemei este întotdeauna sub forma următoare:

avem 2 (sau mai multe) distribuții posibile
avem 1 valoare observată
determinăm cea mai plauzibilă distribuție, pe baza valorii observate

Cu toate acestea, decizia se poate lua într-o varietate de situații:

medicină: un semnal ECG indică o boală sau nu?
business: va cumpăra clientul un produs, sau nu?

Exemplu (pur imaginar)

O persoană sănătoasă are concentrația de trombocite pe ml de sânge distribuită aproximativ $\mathcal{N} \; (\mu=100, \sigma^2 = 20)$.

O persoană suferind de boala B are o valoare mult mai scăzută, distribuită aproximativ $\mathcal{N} \; (30, \sigma^2=10)$.

În urma analizelor de laborator, ai obținut valoarea $r = 79$. Decideți: sănătos sau nu?